- Introduction
-
 -rings
-rings
- Prisms
- Perfect prisms
- The prismatic site and the prismatic cohomology
- The Hodge-Tate comparison
- Extension to the singular case
- Perfections in mixed characteristic
- The etale comparison
-
The
 -de Rham complex
-de Rham complex
-
The
 -crystalline cohomology
-crystalline cohomology
-
 -crystalline comparison and
-crystalline comparison and  -de Rham comparison
-de Rham comparison
- Prismatic cohomology via topological Hochschild homology
These are my live-TeXed notes for Professor Bhargav Bhatt's Eilenberg lectures Geometric aspects of p-adic Hodge theory at Columbia, Fall 2018.
Notice that Bhargav has written up his own notes (read those!) I keep the live-TeXed notes here for the sole purpose of reinforcing my understanding.
09/05/2018
 Introduction
Introduction
The goal of this series to explain prismatic cohomology, which unifies various cohomology theories in  -adic geometry.
-adic geometry.
 Motivation
Motivation
The motivation comes from the classical de Rham comparison theorem.
Notice that RHS is the cohomology of the holomorphic (or algebraic, hence the name "Serre") de Rham complex of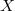 , which depends on the geometry of
, which depends on the geometry of 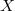 , while LHS only depends on the topology of
, while LHS only depends on the topology of 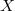 . Explicitly, the isomorphism is given by integration along cycles and each homology class
. Explicitly, the isomorphism is given by integration along cycles and each homology class 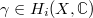 defines an obstruction to integrating
defines an obstruction to integrating 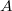 -forms on
-forms on 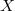 .
.
RHS is rather computable (e.g., by Macaulay) using the defining equation of 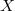 , which helps one to obtain topological information about
, which helps one to obtain topological information about 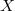 . Conversely, the comparison shows that deforming the complex structure
. Conversely, the comparison shows that deforming the complex structure 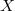 without changing the underlying topology still keeps holomorphic invariants.
without changing the underlying topology still keeps holomorphic invariants.
 cohomology classes (or equivalently,
cohomology classes (or equivalently,  -torsion classes) on
-torsion classes) on 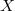 "geometrically"?
"geometrically"?
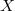 is algebraic, these give obstructions to integrating
is algebraic, these give obstructions to integrating 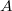 -forms on "
-forms on "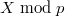 ".
".
 Global statements
Global statements
Let  be a smooth closed subvariety, whose defining equations live in
be a smooth closed subvariety, whose defining equations live in ![$\mathbb{Z}[1/N]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_136422478_-5.gif) . Assume that
. Assume that 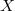 is still smooth mod
is still smooth mod 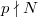 (i.e., good reduction outside
(i.e., good reduction outside  ).
).
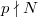 . We have
. We have  Here
Here  is the associated complex analytic manifold,
is the associated complex analytic manifold, 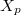 is the reduction of
is the reduction of 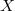 mod
mod  , and
, and 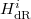 is the algebraic de Rham cohomology.
is the algebraic de Rham cohomology.
- The inequality in Theorem 2 can be strict (examples can be constructed using fibrations with no sections but admitting sections mod
 ). For
). For  large enough, both sides are equal to the dimension of
large enough, both sides are equal to the dimension of  . For a fixed
. For a fixed  , the Euler characteristics of both sides are the same.
, the Euler characteristics of both sides are the same. - The inequality cannot be upgraded to a "naturally defined" subquotient relation: there exists a version of the inequality for mod
 coefficients, and there is an example such that LHS =
coefficients, and there is an example such that LHS =  while RHS =
while RHS =  .
. - The inequality is also valid for any proper smooth formal scheme
 , where
, where  is a
is a  -adic valuation ring (after replacing singular cohomology by etale cohomology). In this case, if
-adic valuation ring (after replacing singular cohomology by etale cohomology). In this case, if  , then the inequality is actually an equality (this recovers earlier results of Faltings, Caruso).
, then the inequality is actually an equality (this recovers earlier results of Faltings, Caruso). - The inequality also holds true for semistable reduction (Cesnavicus, Koshikawa). They basically carried out what we did for the good reduction case.
This gives an algebraic way to control the torsion in singular cohomology.
Conversely, torsion in singular cohomology forces de Rham cohomology to be larger, as in the following example.
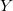 is an Enriques surface in characteristic 2. Then
is an Enriques surface in characteristic 2. Then 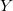 has the form
has the form 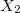 for some Enriques surface
for some Enriques surface 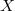 in characteristic 0.
in characteristic 0. 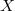 is always a quotient of K3 surface by a fixed point-free involution, so has fundamental group
is always a quotient of K3 surface by a fixed point-free involution, so has fundamental group 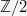 . So the inequality in Theorem 2 implies that
. So the inequality in Theorem 2 implies that 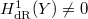 even though
even though 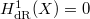 (this recovers an example of Illusie, W. Lang).
(this recovers an example of Illusie, W. Lang).
The strategy of the proof of Theorem 2 is to consider a cohomology theory  valued in
valued in ![$A:=\mathbb{F}_p[ [u] ]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_73302625_-5.gif) -modules (an example of prismatic cohomology), such that
-modules (an example of prismatic cohomology), such that
- There is an identification
![$H^i_A(X)[1/u]=H^i(X^\mathrm{an}, \mathbb{F}_p) \otimes \mathbb{F}_p((t))$](./latex/BhattEilenberg/latex2png-BhattEilenberg_250652060_-5.gif) .
. - There is an injective map
 Notice that a) + b) clearly implies Theorem 2.
Notice that a) + b) clearly implies Theorem 2.
 Local structure of prismatic cohomology
Local structure of prismatic cohomology
Fix a prime  for the rest of the semester (
for the rest of the semester ( is a very good prime for computation in prismatic cohomology!) Set
is a very good prime for computation in prismatic cohomology!) Set ![$A=\mathbb{Z}_p[ [u] ]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_262232022_-5.gif) . Let
. Let  a "Frobenius lift" on
a "Frobenius lift" on 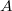 from
from 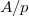 . Let
. Let  be the ideal defining the "diagonal" of
be the ideal defining the "diagonal" of 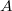 . Let
. Let  be (the
be (the  -adic completion of) a smooth
-adic completion of) a smooth 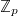 -algebra. Write
-algebra. Write  , and
, and  , where
, where 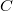 is an algebraic closure of
is an algebraic closure of  . Let
. Let  be the algebraic de Rham complex of
be the algebraic de Rham complex of  .
.
 be the
be the  -adic completion of
-adic completion of ![$\mathbb{Z}_p[x, x^{-1}]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_180353673_-5.gif) . Then
. Then 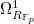 is a free
is a free  -module of rank 1 generated by
-module of rank 1 generated by 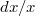 , and higher exterior powers vanish. So we find
, and higher exterior powers vanish. So we find 
 , one can attach an
, one can attach an 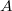 -complex (prismatic complex)
-complex (prismatic complex) 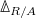 (canonical only in the derived category) and a map
(canonical only in the derived category) and a map  such that
such that
- (de Rham comparison)
 (the diagonal computes the de Rham cohomology of
(the diagonal computes the de Rham cohomology of  ). In particular,
). In particular,  (the origin gives the de Rham cohomology of
(the origin gives the de Rham cohomology of  ).
). - (etale comparison)
 (the
(the  -axis) recovers the
-axis) recovers the 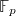 -etale cohomology of
-etale cohomology of  . In between the
. In between the  -axis and the diagonal we obtain the
-axis and the diagonal we obtain the 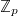 -etale cohomology of
-etale cohomology of  .
. - (Hodge-Tate comparison)
 .
.
- Combining a) and c) recovers the Cartier isomorphism

- This theory globalizes and for
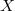 proper, we have the hypercohomology of the resulting complex gives the cohomology theory
proper, we have the hypercohomology of the resulting complex gives the cohomology theory  mentioned before. The (etale comparison) is literally true in this proper case.
mentioned before. The (etale comparison) is literally true in this proper case. - The triple
 is an example of a prism (a commutative ring with a Frobenius lift and a principal ideal which behaves in a particular way with respect to the Frobenius lift). This theory actually works over any prism. For example, one can take
is an example of a prism (a commutative ring with a Frobenius lift and a principal ideal which behaves in a particular way with respect to the Frobenius lift). This theory actually works over any prism. For example, one can take ![$A=\mathbb{Z}_p[[ q-1] ]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_247026286_-5.gif) with
with  , and
, and ![$I=[p]_q$](./latex/BhattEilenberg/latex2png-BhattEilenberg_54395201_-5.gif) , where
, where ![$[p]_q=\frac{q^p-1}{q-1}$](./latex/BhattEilenberg/latex2png-BhattEilenberg_54179731_-8.gif) is the
is the  -analogue of
-analogue of  (which recovers
(which recovers  when
when 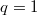 ). Let
). Let  be the
be the  -adic completion of the Laurent polynomial ring over
-adic completion of the Laurent polynomial ring over 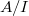 . Then
. Then  In this case the prismatic complex is given by
In this case the prismatic complex is given by  -adic completion of the
-adic completion of the  -deformation (
-deformation ( -de Rham complex)
-de Rham complex) ![$$\Delta_{R/A}=\bigoplus_{i\in \mathbb{Z} }(A x^i \xrightarrow{[i]_q} A x^i dx/x).$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_87666000_.gif) It will take us a while to obtain this explicit formula, as the construction of the prismatic complex is not directly related to
It will take us a while to obtain this explicit formula, as the construction of the prismatic complex is not directly related to  -deformations.
-deformations.
09/17/2018

 -rings
-rings
Last time we tried to make the point that prismatic cohomology is a deformation of de Rham cohomology (traditionally crystalline cohomology is an example of such a deformation). We would like to stress that it is a good idea to also carry along a lift of the Frobenius with the deformation. This leads to the notion of  -rings (Joyal, Buium, Borger...)
-rings (Joyal, Buium, Borger...)
Let  be a (commutative) ring with a map
be a (commutative) ring with a map 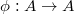 such that
such that  . Then for each
. Then for each  , we have
, we have  . The notion of
. The notion of  -ring is trying to remember
-ring is trying to remember  (rather than
(rather than 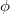 ). Notice that if
). Notice that if  is
is  -torsion-free, then
-torsion-free, then  is a function of
is a function of 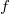 .
.
- If
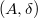 is a
is a  -ring, then
-ring, then  gives a ring map
gives a ring map 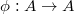 lifting
lifting  .
. - If
 is
is  -torsion-free, then a) gives a bijection between the
-torsion-free, then a) gives a bijection between the  -structures on
-structures on  and endomorphisms
and endomorphisms 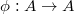 lifting
lifting  on
on 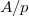 .
.
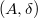 , let us check
, let us check 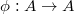 is additive:
is additive: 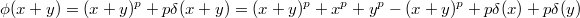 which is equal to
which is equal to  as desired.
¡õ
as desired.
¡õ
- There is a unique
 -ring structure on
-ring structure on  , given by
, given by 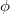 = identity. Then
= identity. Then  . One can check this is the initial object in
. One can check this is the initial object in  -rings.
-rings. - Let
![$A=\mathbb{Z}[x]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_26879790_-5.gif) . Then for any polynomial
. Then for any polynomial ![$g(x)\in \mathbb{Z}[x]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_246174076_-5.gif) , the map
, the map  gives a
gives a  -structure on
-structure on  .
. - Let
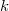 be a perfect field of characteristic
be a perfect field of characteristic  . Then the ring of Witt vectors
. Then the ring of Witt vectors  (the unique
(the unique  -adically complete and
-adically complete and  -torsion-free ring lifting
-torsion-free ring lifting 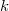 ) with
) with  (induced by
(induced by  on
on 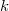 ), is a
), is a  -ring.
-ring. - Let
![$A=\mathbb{Z}[1/p]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_172241998_-5.gif) -algebra. The any ring map
-algebra. The any ring map 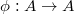 gives a
gives a  -ring on
-ring on  (as we can write down
(as we can write down  by dividing
by dividing  ).
). - Let
![$A=\mathbb{Z}[x]/(px, x^p)$](./latex/BhattEilenberg/latex2png-BhattEilenberg_153945909_-5.gif) (not
(not  -torsion-free). Then there exists a unique
-torsion-free). Then there exists a unique  -structure on
-structure on  with
with 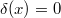 (the existence would not be true without quotienting
(the existence would not be true without quotienting  ). So there can be
). So there can be  -torsion in
-torsion in  -ring. However,
-ring. However,  cannot kill 1 as the following lemma shows.
cannot kill 1 as the following lemma shows.
 -ring
-ring  where
where 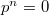 for some
for some 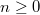 (think:
(think:  is a "
is a " -derivation", which lowers the order of
-derivation", which lowers the order of  -adic vanishing by 1).
-adic vanishing by 1).
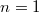 , and
, and  is a
is a 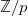 -algebra with a
-algebra with a  -structure. Apply
-structure. Apply  to
to 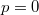 we obtain
we obtain 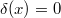 . On the other hand
. On the other hand 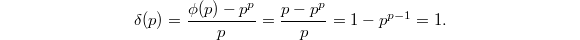 Hence
Hence 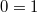 and
and  is the zero ring.
¡õ
is the zero ring.
¡õ
 in a
in a  -ring
-ring  has rank 1 if
has rank 1 if 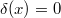 . This terminology is motivated by
. This terminology is motivated by  -theory where
-theory where 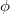 comes from the Adams operator and when
comes from the Adams operator and when 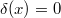 ,
, 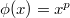 is what the Adams operator does on line bundles.
is what the Adams operator does on line bundles.
 The category of
The category of  -rings
-rings
Reference: C. Rezk, Etale extensions of  -rings.
-rings.
 , we define a new ring
, we define a new ring 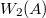 as follows: as a set
as follows: as a set 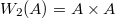 , with addition
, with addition 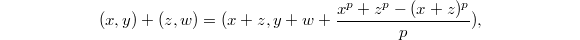 and multiplication
and multiplication 
Using these formulas, it is easy to check the following lemma.
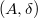 be a
be a  -ring. Then the map
-ring. Then the map  is a ring map lifting the identity after the restriction map
is a ring map lifting the identity after the restriction map  And conversely, any section of the restriction map
And conversely, any section of the restriction map 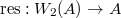 gives a
gives a  -structure on
-structure on  .
.
 -rings has all limits and colimits, and they are computed on the underlying rings (i.e., limits and colimits commutes with forgetful functor to rings).
-rings has all limits and colimits, and they are computed on the underlying rings (i.e., limits and colimits commutes with forgetful functor to rings).
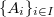 is a diagram of
is a diagram of  -rings. They give maps
-rings. They give maps 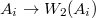 compatible in
compatible in 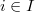 . We obtain a map
. We obtain a map 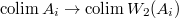 . There is also a canonical map
. There is also a canonical map 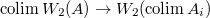 (as
(as 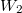 is a functor). One can check the composition gives a
is a functor). One can check the composition gives a  -structure on
-structure on 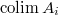 .
¡õ
.
¡õ
 (Joyal). The left adjoint is the free object functor described as follows.
(Joyal). The left adjoint is the free object functor described as follows.
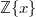 is a
is a  -ring: the map
-ring: the map  extends uniquely to a Frobenius lift on
extends uniquely to a Frobenius lift on 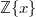 . This construction works for the universal property by looking at what
. This construction works for the universal property by looking at what  does on the generator.
does on the generator.
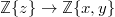 say sending
say sending 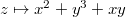 (or any other polynomial). Pushing-out along
(or any other polynomial). Pushing-out along 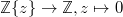 we obtain a
we obtain a  -ring
-ring 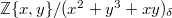 in which
in which 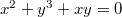 . However, it is hard to explicitly compute
. However, it is hard to explicitly compute 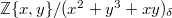 , as free
, as free  -rings are of infinite type.
-rings are of infinite type.
 be a
be a  -ring. Let
-ring. Let  be a multiplicative subset such that
be a multiplicative subset such that  . Then
. Then  has a unique
has a unique  -structure compatible with that of
-structure compatible with that of  .
.
 is
is  -torsion-free. Then there exists a unique map
-torsion-free. Then there exists a unique map  compatible with
compatible with 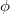 on
on  . Since
. Since 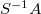 is also
is also  -torsion-free, and
-torsion-free, and  is a lift of Frobenius on
is a lift of Frobenius on 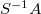 , we obtain a unique
, we obtain a unique  -structure on
-structure on 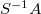 .
.
In general  not
not  -torsion-free but we can reduce to the
-torsion-free but we can reduce to the  -torsion-free case (this is a trick we will often use). One can find a free
-torsion-free case (this is a trick we will often use). One can find a free  -ring
-ring  (
( -torsion-free) and a multiplicative set
-torsion-free) and a multiplicative set  such that
such that  and a surjection
and a surjection  which takes
which takes  to
to 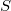 . We then obtain a pushout diagram
. We then obtain a pushout diagram ![$$\xymatrix{ F \ar[r] \ar[d] & T^{-1}F \ar[d]\\ A \ar[r] & S^{-1}A}$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_95407113_.gif) Now we use a colimit of
Now we use a colimit of  -rings is a
-rings is a  -ring to see that
-ring to see that 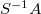 is also a
is also a  -ring. And one can check the
-ring. And one can check the  -structure is independent of the choice of
-structure is independent of the choice of  and
and  .
¡õ
.
¡õ
 Perfect
Perfect  -rings
-rings
Now we discuss a property that is special to the category of  -rings.
-rings.
Perfect  -rings are essentially perfect algebras in characteristic
-rings are essentially perfect algebras in characteristic  :
:
- Perfect and
 -adically complete
-adically complete  -rings.
-rings. - Perfect
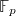 -algebras.
-algebras.
The equivalence is via  , and
, and  .
.
The key lemma to prove this theorem is the following:
 is a
is a  -adically complete
-adically complete  -ring and
-ring and 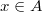 is a
is a  -torsion element, then
-torsion element, then 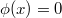 . In particular, perfect
. In particular, perfect  -rings are
-rings are  -torsion-free.
-torsion-free.
 to
to 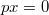 , we obtain
, we obtain  Since
Since  is
is  -adically complete, we know that
-adically complete, we know that 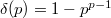 is a unit. To prove
is a unit. To prove 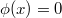 if suffice to show that
if suffice to show that 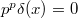 . But
. But  Here the last equality is due to
Here the last equality is due to 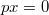 .
¡õ
.
¡õ
09/24/2018
We recall the following standard construction.
 be a perfect
be a perfect 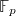 -algebra. There exists a unique multiplicative map, the Teichmuller lift,
-algebra. There exists a unique multiplicative map, the Teichmuller lift, ![$[\cdot]: R\rightarrow W(R)$](./latex/BhattEilenberg/latex2png-BhattEilenberg_59924285_-5.gif) splitting the projection
splitting the projection 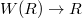 . Given
. Given 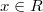 , we define
, we define ![$[x]\in W(R)/p^{n+1}$](./latex/BhattEilenberg/latex2png-BhattEilenberg_202815441_-5.gif) to be
to be 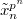 , where
, where 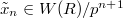 is some lift of
is some lift of 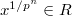 . One can check this is well-defined using essentially the binomial identity:
. One can check this is well-defined using essentially the binomial identity:
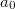 to be the image of
to be the image of 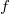 in
in  ,
, 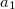 to be the image of
to be the image of ![$(f-[a_0])/p$](./latex/BhattEilenberg/latex2png-BhattEilenberg_139289402_-5.gif) and so on.
¡õ
and so on.
¡õ
These  's are called the Teichmuller coordinates of
's are called the Teichmuller coordinates of 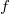 (though these coordinates does not respect the ring structure).
(though these coordinates does not respect the ring structure).
 Distinguished elements
Distinguished elements
For a commutative ring  , we write
, we write  to be the Jacobson radical of
to be the Jacobson radical of  . A more useful way to think about it is that it consists of "small" elements
. A more useful way to think about it is that it consists of "small" elements  We will always assume that
We will always assume that  (so all other prime numbers are invertible in
(so all other prime numbers are invertible in  ).
).
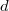 in a
in a  -ring
-ring  is distinguished (or primitive) if
is distinguished (or primitive) if 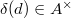 (this terminology dates back to Fontaine). Since
(this terminology dates back to Fontaine). Since 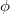 is a ring map, we know that if
is a ring map, we know that if 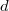 is distinguished, then
is distinguished, then 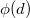 is also distinguished.
is also distinguished.
A distinguished element can be thought of as a "deformation" of  .
.
- (crystalline cohomology)
 . Then
. Then  is distinguished as
is distinguished as  . In fact,
. In fact,  is distinguished in any
is distinguished in any  -ring
-ring  .
. - (
 -de Rham cohomology)
-de Rham cohomology) ![$A=\mathbb{Z}_p[ [q-1] ]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_247252846_-5.gif) (
( ). Then
). Then ![$d=[p]_q$](./latex/BhattEilenberg/latex2png-BhattEilenberg_54391873_-5.gif) is distinguished. In fact, consider the map
is distinguished. In fact, consider the map  . This a
. This a  -map. Moreover,
-map. Moreover, 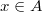 is a unit if and only if
is a unit if and only if  is a unit (as
is a unit (as  is topologically nilpotent). Now
is topologically nilpotent). Now  , so
, so  is a unit, hence
is a unit, hence 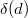 is a unit. The intuition here is that specializing to
is a unit. The intuition here is that specializing to 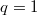 allows one check to an element is distinguished more easily.
allows one check to an element is distinguished more easily. - (Breuil-Kisin cohomology)
![$A=\mathbb{Z}_p[ [u]]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_255038030_-5.gif) (
( ). Then
). Then  is distinguished. One can check this using the specialization
is distinguished. One can check this using the specialization  . (here
. (here  is even "smaller" than
is even "smaller" than  as
as 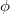 contracts
contracts  ).
). - (
 -cohomology)
-cohomology)  -adic completion of
-adic completion of ![$\mathbb{Z}_p[q, q^{1/p},q^{1/p^2},\ldots,]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_244081363_-5.gif) (
( ). Then
). Then ![$d=[p]_q$](./latex/BhattEilenberg/latex2png-BhattEilenberg_54391873_-5.gif) is distinguished (from b)).
is distinguished (from b)).
In all these examples we know how to deform the de Rham cohomology from 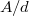 to
to  , but the constructions are different (at least three constructions). Our goal is to uniforms these different constructions.
, but the constructions are different (at least three constructions). Our goal is to uniforms these different constructions.
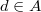 be a distinguished element in a
be a distinguished element in a  -ring. Assume
-ring. Assume 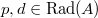 . Then
. Then 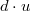 is also distinguished for any unit
is also distinguished for any unit  .
.
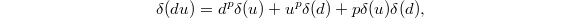 the first and third terms are in
the first and third terms are in  (as
(as  and
and  are), and the second term is a unit (as
are), and the second term is a unit (as 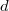 is distinguished), we know that
is distinguished), we know that 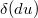 is also a unit.
¡õ
is also a unit.
¡õ
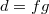 is distinguished. Assume
is distinguished. Assume  . Then
. Then 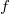 is distinguished and
is distinguished and  is unit. (In particular, in a
is unit. (In particular, in a  -ring there can not be a square root of
-ring there can not be a square root of  ).
).
 Again the first and third terms are in
Again the first and third terms are in 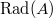 . So the second term
. So the second term 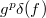 is a unit, and hence
is a unit, and hence  is a unit and
is a unit and 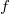 is distinguished.
¡õ
is distinguished.
¡õ
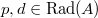 . Then
. Then 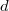 is distinguished if and only if
is distinguished if and only if 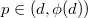 . In particular, the condition that
. In particular, the condition that 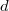 is distinguished only depends on the ideal
is distinguished only depends on the ideal 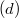 .
.
 says that the intersection of the two closed subschemes defined by
says that the intersection of the two closed subschemes defined by 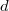 and
and 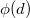 is completely supported in characteristic
is completely supported in characteristic  .
.
 depends only of
depends only of 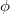 (which uses less information than remembering
(which uses less information than remembering  ).
).
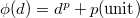 . So if
. So if 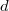 is distinguished, then
is distinguished, then 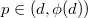 . Conversely, write
. Conversely, write 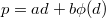 . We need to show that
. We need to show that 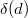 is a unit. This is equivalent to that
is a unit. This is equivalent to that 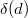 is a unit in
is a unit in 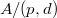 , or equivalently
, or equivalently 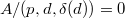 . We will proceed by contradiction. We may assume that
. We will proceed by contradiction. We may assume that 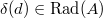 (after localizing along the locus where
(after localizing along the locus where 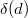 is not a unit). Then
is not a unit). Then  for some
for some 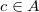 . So
. So  Notice that RHS is distinguished as
Notice that RHS is distinguished as 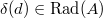 and so
and so 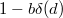 is a unit. Thus the irreducibility lemma (Lemma 10) implies that
is a unit. Thus the irreducibility lemma (Lemma 10) implies that 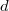 is distinguished, a contradiction.
¡õ
is distinguished, a contradiction.
¡õ
 be a perfect
be a perfect 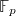 -algebra.
-algebra.
- An element
 is distinguished if and only if
is distinguished if and only if  is a unit, where
is a unit, where ![$d=\sum_{i\ge0}[a_i]p^i$](./latex/BhattEilenberg/latex2png-BhattEilenberg_23473476_-7.gif) is the Teichmuller expansion.
is the Teichmuller expansion. - Any distinguished element of
 is a non zero divisor.
is a non zero divisor. - If
 is distinguished, then
is distinguished, then  has bounded
has bounded  -power-torsion. In fact,
-power-torsion. In fact, ![$W(R)/(d)[p^\infty]=W(R)/(d)[p]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_103448541_-5.gif) .
.
 Digression: derived completions
Digression: derived completions
A prism will be a  -ring together with an ideal that is locally cut out by distinguished elements (but not necessarily globally). It is also more convenient to assume that it is "complete" along the ideal. We thus need a good notion of completion (for non-noetherian rings).
-ring together with an ideal that is locally cut out by distinguished elements (but not necessarily globally). It is also more convenient to assume that it is "complete" along the ideal. We thus need a good notion of completion (for non-noetherian rings).
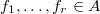 and
and 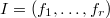 . An
. An  -complex
-complex 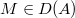 is derived
is derived 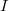 -complete if for any
-complete if for any 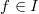 ,
, 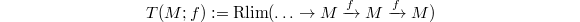 is 0 in
is 0 in 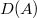 (here
(here 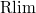 is the right derived functor of the inverse limit functor). This is equivalent to
is the right derived functor of the inverse limit functor). This is equivalent to ![$$M \cong \hat M:=\mathrm{Rlim}_n M \otimes^L_{\mathbb{Z}[x_1,\ldots, x_r]} \otimes \mathbb{Z}[x_1,\ldots, x_r]/(x_1^n,\ldots, x_r^n),$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_242409869_.gif) where
where  acts on
acts on 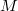 by
by 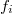 . Notice that the completion here is less naive (using the noetherian ring
. Notice that the completion here is less naive (using the noetherian ring ![$\mathbb{Z}[x_1,\ldots,x_r]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_126098261_-5.gif) instead of
instead of  ). See notes for the rest of the assertions.
). See notes for the rest of the assertions.
- All derived
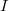 -complete
-complete  -complexes form a triangulated subcategory closed under product. It has a left adjoint
-complexes form a triangulated subcategory closed under product. It has a left adjoint  .
. 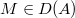 is derived
is derived 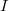 -complete if and only if each
-complete if and only if each  (put in degree 0) is derived
(put in degree 0) is derived 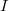 -complete.
-complete.- All derived
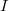 -complete
-complete  -modules form an abelian subcategory of all
-modules form an abelian subcategory of all  -modules.
-modules. - (Derived Nakayama) Assume
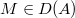 is derived
is derived 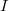 -complete. Then
-complete. Then  if and only if
if and only if  .
.
10/08/2018
 Prisms
Prisms
Recall (Lemma 11):
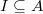 be a locally principal ideal. Assume
be a locally principal ideal. Assume  . Then the following are equivalent:
. Then the following are equivalent:
 .
.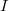 is (Zariski) locally generated by distinguished elements.
is (Zariski) locally generated by distinguished elements. (use
(use  ).
).
Prisms will be the objects of the prism site.
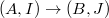 of prisms (a ring map
of prisms (a ring map 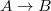 sending
sending 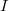 into
into 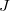 ) is (faithfully) flat if
) is (faithfully) flat if 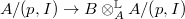 is (faithfully) flat. Here flat means that the target complex has cohomology only in degree 0 and this cohomology is flat over the source.
is (faithfully) flat. Here flat means that the target complex has cohomology only in degree 0 and this cohomology is flat over the source.
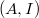 is called perfect if
is called perfect if  is perfect; crystalline if
is perfect; crystalline if 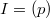 ; bounded if
; bounded if 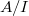 has bounded
has bounded 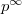 -torsion. Every prism we will encounter will be bounded.
-torsion. Every prism we will encounter will be bounded.
- Any
 -torsionfree and
-torsionfree and  -adically complete
-adically complete  -ring
-ring  gives a prism
gives a prism  .
. - Perfect prisms = perfectoid rings.
We don't know a natural example of a prism of where 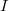 is locally principal but not principal (though abstract examples exist). The following lemma shows that
is locally principal but not principal (though abstract examples exist). The following lemma shows that 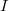 is not far from principal.
is not far from principal.
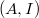 be a prism. Then
be a prism. Then 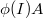 is principal and any generator is a distinguished element. In particular,
is principal and any generator is a distinguished element. In particular, ![$I\in\Pic(A)[p]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_200534726_-5.gif) (exercise).
(exercise).
 , where
, where 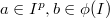 . Then one can check that
. Then one can check that 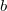 is a generator of
is a generator of 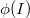 . The key is to use the irreducibility lemma (Lemma 10) for distinguished elements (see notes).
¡õ
. The key is to use the irreducibility lemma (Lemma 10) for distinguished elements (see notes).
¡õ
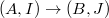 be a map of prisms. Then
be a map of prisms. Then 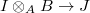 is an isomorphism (so a map of prisms is determined on the underlying
is an isomorphism (so a map of prisms is determined on the underlying  -rings).
-rings).
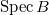 .
¡õ
.
¡õ
 Perfect prisms
Perfect prisms
- Let
 be a perfect and
be a perfect and  -adically complete
-adically complete  -ring, and
-ring, and 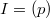 . Then
. Then  for a perfect
for a perfect 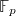 -algebra
-algebra  and
and  (Theorem 4). So any perfect
(Theorem 4). So any perfect 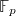 -algebra is perfectoid.
-algebra is perfectoid. ![$A=\mathbb{Z}_p[X^{1/p^\infty}]^{\wedge}_{(p,X)}$](./latex/BhattEilenberg/latex2png-BhattEilenberg_158199140_-8.gif) with
with  is a
is a  -torsionfree
-torsionfree  -ring, and
-ring, and  is generated by a distinguished element. So
is generated by a distinguished element. So ![$R=A/I=\mathbb{Z}_p[p^{1/p^\infty}]^{\wedge}_{(p)}$](./latex/BhattEilenberg/latex2png-BhattEilenberg_194245821_-8.gif) is a perfectoid ring.
is a perfectoid ring.
 be a perfect
be a perfect 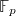 -algebra. Let
-algebra. Let 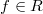 . Then
. Then ![$R[f^\infty]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_157529198_-5.gif) (
(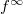 -torsion in
-torsion in  ) is equal to
) is equal to ![$R[f^{1/p^n}]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_183687289_-5.gif) for any
for any  . (The latter is killed by a small power of
. (The latter is killed by a small power of 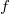 , known as an almost zero module).
, known as an almost zero module).
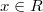 such that
such that 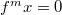 for some
for some  . So
. So 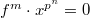 for any
for any  . By reducedness we obtain
. By reducedness we obtain 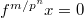 for any
for any 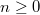 .
¡õ
.
¡õ
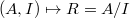 gives an equivalence between the category of perfect prisms and the category of perfectoid rings.
gives an equivalence between the category of perfect prisms and the category of perfectoid rings.
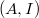 form
form 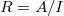 . We claim that
. We claim that 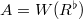 , where
, where  (a perfect
(a perfect 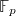 -algebra) is Fontaine's tilting functor.
-algebra) is Fontaine's tilting functor.
Choose  a generator. Then
a generator. Then 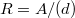 and
and  . As
. As 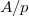 is a perfect
is a perfect 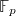 -algebra, we have an identification of the tower
-algebra, we have an identification of the tower  with the tower
with the tower  Taking inverse limits we obtain
Taking inverse limits we obtain  But
But  is isomorphic to
is isomorphic to 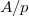 because
because 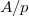 is
is 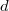 -complete (derived completion and usual completion are the same since
-complete (derived completion and usual completion are the same since 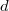 -torsion is bounded). Therefore
-torsion is bounded). Therefore  . See the notes for the identification of
. See the notes for the identification of 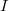 as the kernel of
as the kernel of  .
¡õ
.
¡õ
![$R=\mathbb{Z}_p[p^{1/p^\infty}]_{(p)}^\wedge$](./latex/BhattEilenberg/latex2png-BhattEilenberg_3412864_-8.gif) . Then
. Then ![$A_\mathrm{inf}(R)=\mathbb{Z}_p[X^{1/p^\infty}]_{(p,X)}^\wedge$](./latex/BhattEilenberg/latex2png-BhattEilenberg_33880483_-8.gif) (a "2-dimensional" object), and
(a "2-dimensional" object), and 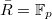 (all nilpotents in
(all nilpotents in 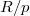 are killed when passing to the perfection).
are killed when passing to the perfection).
 be a perfectoid ring. Then
be a perfectoid ring. Then
- The Frobenius
 is surjective.
is surjective. - There exists
 such that
such that  and
and  .
. - The radical
 is a flat ideal and
is a flat ideal and  (the beginning of almost math).
(the beginning of almost math). ![$R[p^\infty]=R[p]=R[\sqrt{pR}].$](./latex/BhattEilenberg/latex2png-BhattEilenberg_42210126_-5.gif)
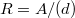 and
and 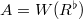 . (a) is clear since Frobenius on
. (a) is clear since Frobenius on 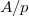 is surjective and
is surjective and 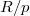 is a quotient of
is a quotient of 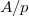 . For (b), write
. For (b), write ![$d=[a_0]+[a_1]p+\cdots$](./latex/BhattEilenberg/latex2png-BhattEilenberg_225544096_-5.gif) , where
, where 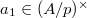 . So we may write
. So we may write![$d=[a_0]-pu$](./latex/BhattEilenberg/latex2png-BhattEilenberg_164782904_-5.gif) , where
, where 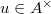 . Thus in
. Thus in 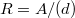 , we have
, we have ![$[a_0]=pu$](./latex/BhattEilenberg/latex2png-BhattEilenberg_235314376_-5.gif) . We may then take
. We may then take ![$\pi=[a_0^{1/p}]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_212105275_-5.gif) (the Teichmuller map is multiplicative). For (c), we claim that
(the Teichmuller map is multiplicative). For (c), we claim that ![$([a_0^{1/p^n}]_{n\ge1})=\sqrt{pR}$](./latex/BhattEilenberg/latex2png-BhattEilenberg_131483371_-5.gif) . It suffices to show that
. It suffices to show that ![$R/([a_0^{1/p^n}]_{n\ge1})$](./latex/BhattEilenberg/latex2png-BhattEilenberg_175854054_-5.gif) is reduced (equivalently, perfect). This follows from the general fact that if
is reduced (equivalently, perfect). This follows from the general fact that if 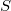 is a perfect
is a perfect 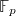 -algebra, and
-algebra, and 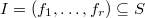 an ideal. Then
an ideal. Then 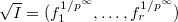 .
¡õ
.
¡õ
- If
 ,
,  are maps of perfectoid rings. Then
are maps of perfectoid rings. Then  is perfectoid (no Tor even without flatness assumptions in the perfectoid world!)
is perfectoid (no Tor even without flatness assumptions in the perfectoid world!) - If
 is perfectoid, then
is perfectoid, then ![$S=R/R[\sqrt{pR}]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_118962818_-5.gif) is perfectoid (and
is perfectoid (and  -torsionfree), and
-torsionfree), and ![$$\xymatrix{R \ar[r]\ar[d] & S \ar[d] \\ \bar R \ar[r] & \bar S }$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_240697145_.gif) is a pullback diagram. So one can build any perfectoid ring using a
is a pullback diagram. So one can build any perfectoid ring using a  -torsionfree perfectoid ring
-torsionfree perfectoid ring 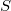 and a perfect
and a perfect 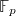 -algebra
-algebra  . In particular,
. In particular,  is reduced.
is reduced.
10/15/2018
 The prismatic site and the prismatic cohomology
The prismatic site and the prismatic cohomology
We will let 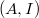 be a "base" prism. Assume
be a "base" prism. Assume  is generated by a distinguished element and
is generated by a distinguished element and ![$A/I[p^\infty]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_261245200_-5.gif) is bounded.
is bounded.
- (crystalline) Let
 be any
be any  -torsionfree,
-torsionfree,  -complete
-complete  -ring and
-ring and 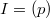 .
. - (Breuil-Kisin) Let
![$A=\mathbb{Z}_p[ [u] ]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_262232022_-5.gif) with
with  and
and  , where
, where  is any Eisenstein polynomial (e.g.
is any Eisenstein polynomial (e.g.  ).
). - (
 ) Let
) Let  be a perfectoid ring and
be a perfectoid ring and  .
. - (
 -de Rham) Let
-de Rham) Let ![$A=\mathbb{Z}_p[ [q-1]]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_189640794_-5.gif) with
with  , and
, and ![$I=[p]_q$](./latex/BhattEilenberg/latex2png-BhattEilenberg_54395201_-5.gif) .
.
Let  be a formally smooth
be a formally smooth 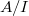 -algebra (e.g., the
-algebra (e.g., the  -adic completion of a smooth
-adic completion of a smooth 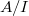 -algebra). Our goal is to construct an object
-algebra). Our goal is to construct an object  such that
such that
 gives differential forms on
gives differential forms on  relative to
relative to 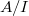 .
.![$\Delta_{R/A}[1/p]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_83547056_-6.gif) is related to etale cohomology of
is related to etale cohomology of ![$R[1/p]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_64986512_-5.gif) .
.
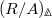 of
of  relative to
relative to  consists of prisms
consists of prisms 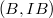 over
over  together with a map
together with a map 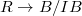 over
over 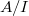 . (Notice the direction of the map is different from the crystalline site). Pictorially we have
. (Notice the direction of the map is different from the crystalline site). Pictorially we have ![$$\xymatrix{A \ar[d] \ar[rr] & & B \ar[d] \\ A/I \ar[r] & R \ar[r] & B/IB.}$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_13496920_.gif) We will write it as
We will write it as 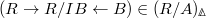 .
.
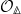 and
and  on
on 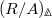 given by sending
given by sending 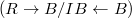 to
to  (an
(an  -algebra over
-algebra over  ) and
) and 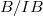 (an
(an  -algebra) respectively. (In the perfectoid case
-algebra) respectively. (In the perfectoid case 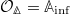 and
and  ).
).
- One should really define
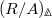 as the opposite of the above definition, so
as the opposite of the above definition, so 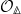 and
and  are presheaves (we will focus on the affine case as the gluing will be easy).
are presheaves (we will focus on the affine case as the gluing will be easy). - Even though the definition of
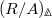 makes sense for any
makes sense for any  , the theory works best for
, the theory works best for  formally smooth (or locally complete intersection). The same comment applies to the crystalline site.
formally smooth (or locally complete intersection). The same comment applies to the crystalline site.
- Let
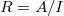 . Then
. Then 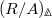 is the category of prisms over
is the category of prisms over 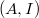 . In particular, it has a initial object and hence the prismatic cohomology will be simply
. In particular, it has a initial object and hence the prismatic cohomology will be simply  .
. - Let
 (the
(the  -adic completion of
-adic completion of ![$A/I[x]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_262169515_-5.gif) ). Then there is no initial object. There exists
). Then there is no initial object. There exists  formally smooth lift of
formally smooth lift of  together with a
together with a  -structure on
-structure on  (e.g.,
(e.g., ![$\tilde R=A[x]^\wedge$](./latex/BhattEilenberg/latex2png-BhattEilenberg_141711451_-5.gif) and
and 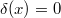 . Then
. Then  . (One can also do the same for any
. (One can also do the same for any  ).
).
 is defined to be
is defined to be  It admits a Frobenius action
It admits a Frobenius action 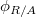 (as the category
(as the category 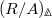 admits a Frobenius action).
admits a Frobenius action).
 is defined to be
is defined to be 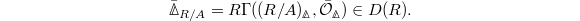 It no longer has the Frobenius action (but is linear over the larger ring
It no longer has the Frobenius action (but is linear over the larger ring  ).
).
These both are commutative algebra objects.
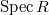 goes through
goes through  and outputs various different cohomology theory:
and outputs various different cohomology theory:

 , we know that we have (a quasi-isomorphism)
, we know that we have (a quasi-isomorphism)  . Since everything is complete, we can detect many things (e.g. vanishing) of
. Since everything is complete, we can detect many things (e.g. vanishing) of 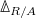 using
using 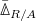 .
.
 The Hodge-Tate comparison
The Hodge-Tate comparison
Let  be a map of commutative rings. We have an algebraic de Rham complex
be a map of commutative rings. We have an algebraic de Rham complex  We view it as a strictly commutative differential graded
We view it as a strictly commutative differential graded  -algebra:
-algebra:
- (graded commutative)
 .
. - (strictly graded commutative)
 if
if  is odd (which only matters in characteristic 2).
is odd (which only matters in characteristic 2).
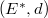 be a graded commutative
be a graded commutative  -dga. Assume we have a map
-dga. Assume we have a map 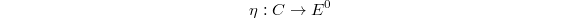 of
of  -algebras. Further assume that for any
-algebras. Further assume that for any 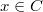 ,
, 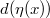 squares to 0. Then there exists a unique extension of
squares to 0. Then there exists a unique extension of 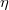 to graded commutative
to graded commutative  -dgas,
-dgas, 
We have a Bockstein exact sequence of sheaves on 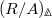 ,
,  Thus we obtain a Bockstein differential
Thus we obtain a Bockstein differential  In this way we obtain a graded commutative
In this way we obtain a graded commutative 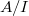 -dga
-dga  . We also have
. We also have  (by
(by  -algebra structure). One can also show that for any
-algebra structure). One can also show that for any 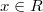 ,
,  squares to 0. Thus by the universal property of the de Rham complex, we obtain a map from the de Rham complex to the Hodge-Tate complex:
squares to 0. Thus by the universal property of the de Rham complex, we obtain a map from the de Rham complex to the Hodge-Tate complex: 
 depends on the choice of
depends on the choice of 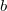 . There is a way to avoid this dependence (which introduces certain Breuil-Kisin twists).
. There is a way to avoid this dependence (which introduces certain Breuil-Kisin twists).
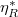 is an isomorphism (as genuine complexes). In particular,
is an isomorphism (as genuine complexes). In particular, 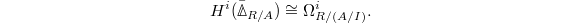 And so
And so 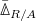 can be represented by a perfect complex (this is the source of finiteness in the global situation).
can be represented by a perfect complex (this is the source of finiteness in the global situation).
- The Hodge-Tate comparison gives the Cartier isomorphism when
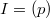 (without the extra Frobenius twist).
(without the extra Frobenius twist). - One can work out the Hodge-Tate comparison explicitly for the
 -de Rham complex (see notes).
-de Rham complex (see notes). - One can deduce from the Hodge-Tate comparison theorem the Hodge-Tate decomposition for the etale cohomology of smooth projective variety
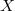 over a
over a  -adic field
-adic field  :
: 
How to compute cohomology of categories? It turns out to be extremely simple.
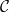 be a small category. Let
be a small category. Let 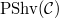 be the category of presheaves on
be the category of presheaves on 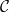 . Then
. Then 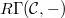 is the derived functor
is the derived functor 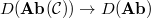 of
of 
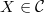 that is weakly final (i.e.,
that is weakly final (i.e., 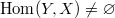 for any
for any 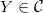 ). Assume that
). Assume that 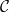 has finite nonempty product. Then
has finite nonempty product. Then 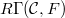 is calculated by
is calculated by 
So in order to compute the cohomology of the prismatic complex, it suffices to find a weakly final object and compute its self-products.
We denote this universal  by
by  (think: the universal prism where
(think: the universal prism where 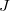 becomes divisible by
becomes divisible by 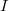 ).
).
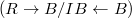 and
and 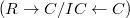 be two objects in
be two objects in 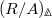 . Set
. Set 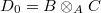 . We have two maps
. We have two maps 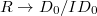 via
via 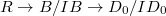 (and similarly for
(and similarly for 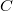 ), which are not necessarily the same. ; Let
), which are not necessarily the same. ; Let  and let
and let 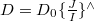 , then the two maps becomes the same in
, then the two maps becomes the same in 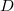 . Then
. Then 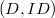 works.
¡õ
works.
¡õ
10/22/2018
The goal today is to sketch a proof of the Hodge-Tate comparison theorem, which is divided into two steps.
- If
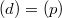 (characteristic
(characteristic  case), prove the crystalline comparison for
case), prove the crystalline comparison for 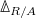 (before reduction).
(before reduction). - Use the Cartier isomorphism when
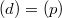 to deduce the Hodge-Tate comparison theorem in general.
to deduce the Hodge-Tate comparison theorem in general.
 Reminder on crystalline cohomology
Reminder on crystalline cohomology
Fix a  -torsionfree ring
-torsionfree ring  , and a smooth
, and a smooth 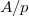 -algebra
-algebra  .
.
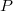 be a (ind)-smooth
be a (ind)-smooth  -algebra. Fix a surjection
-algebra. Fix a surjection  over
over  . (think: embed
. (think: embed 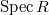 into a smooth affine space.) Let
into a smooth affine space.) Let 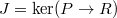 . The divided power envelope of
. The divided power envelope of 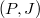 is defined to be
is defined to be ![$$D_J(P)=P[\{\frac{x^n}{n!}\}_{n\ge1, x\in J}]^\wedge$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_63739524_.gif) (
( -adic completion), where
-adic completion), where ![$P[\{\frac{x^n}{n!}\}_{n\ge1, x\in J}]\subseteq P[1/p]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_219550265_-6.gif) . (This is the characteristic
. (This is the characteristic  analogue of allowing integration of power series in
analogue of allowing integration of power series in 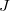 .)
.)
One can check that there exists an induced surjection  with kernel having divided powers. The map
with kernel having divided powers. The map  is universal with this property (hence the name envelope).
is universal with this property (hence the name envelope).
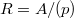 ,
, ![$P=A[x]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_262169261_-5.gif) , and
, and 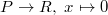 . Then
. Then 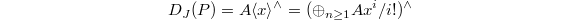 is the divided power polynomial ring. One can check that
is the divided power polynomial ring. One can check that 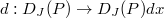 has the cohomology of a point (
has the cohomology of a point (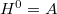 ,
, 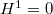 ). This is the characteristic
). This is the characteristic  analogue of the Poincare lemma.
analogue of the Poincare lemma.
 with
with  (ind-)smooth over
(ind-)smooth over  . Let
. Let 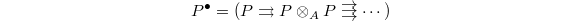 a cosimplicial
a cosimplicial  -algebra. We have an induced surjection
-algebra. We have an induced surjection  with kernel
with kernel 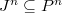 for any
for any  . In this way we obtain an ideal
. In this way we obtain an ideal 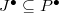 . We define
. We define 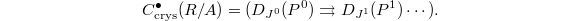 (think: geometrically embed a singular space into powers of a smooth affine space and look at its tubular neighborhoods). Define
(think: geometrically embed a singular space into powers of a smooth affine space and look at its tubular neighborhoods). Define 
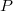 is a smooth lift of
is a smooth lift of  to
to  . Then
. Then  In particular, the de Rham complex on LHS is independent of the lift
In particular, the de Rham complex on LHS is independent of the lift 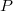 .
.
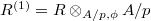 be the Frobenius twist of
be the Frobenius twist of  . So the absolute Frobenius
. So the absolute Frobenius 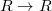 factors as
factors as 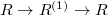 , where the relative Frobenius
, where the relative Frobenius 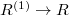 is
is 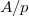 -linear. Notice that
-linear. Notice that 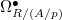 is an
is an  -linear complex (by the Leibniz rule we have
-linear complex (by the Leibniz rule we have 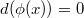 for
for 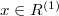 ). We have a map
). We have a map 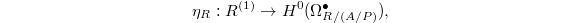 and also have a Bockstein differential
and also have a Bockstein differential  So by the universal property (Lemma 17), we obtain a map of strictly graded commutative dgas,
So by the universal property (Lemma 17), we obtain a map of strictly graded commutative dgas, 
 Relating divided powers to
Relating divided powers to  -structures
-structures
 be a
be a  -torsionfree
-torsionfree  -rings. Let
-rings. Let 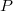 be an (ind-)smooth
be an (ind-)smooth  -algebra over
-algebra over  . Let
. Let 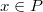 such that
such that  is a non-zero-divisor on
is a non-zero-divisor on 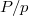 . Then
. Then 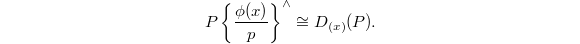 Here LHS means formally adjoining in
Here LHS means formally adjoining in  -rings, and the RHS is the divided power envelope.
-rings, and the RHS is the divided power envelope.
 over
over 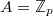 . We have a pushout diagram
. We have a pushout diagram ![$$\xymatrix{\mathbb{Z}_p\{z\} \ar[r] \ar[d]^{z\mapsto \phi(x)} & \mathbb{Z}_p\{z,y\}/(py-z)_\delta=\mathbb{Z}_p\{y\} \ar[d] \\ \mathbb{Z}_p\{x\} \ar[r] & P\{\phi(x)/p\}.}$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_226256642_.gif) Notice that the left vertical arrow is faithfully flat, and hence the right vertical arrow is faithfully flat, thus
Notice that the left vertical arrow is faithfully flat, and hence the right vertical arrow is faithfully flat, thus 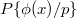 is
is  -torsionfree.
-torsionfree.
The next goal is to identify ![$C=P\{\phi(x)/p\}\subseteq P[1/p]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_82372877_-5.gif) with
with ![$D=P[\{x^n/n!\}]\subseteq P[1/p]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_115545379_-5.gif) . First, by
. First, by  we obtain that
we obtain that ![$$C=P\{x^p/p\}\subseteq P[1/p],$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_30116616_.gif) hence
hence  . To check that
. To check that  , by induction it suffices to show that if
, by induction it suffices to show that if 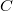 is any
is any  -torsionfree
-torsionfree  -ring, and
-ring, and  such that
such that  , then
, then  . In fact,
. In fact,  The second term has the same
The second term has the same  -adic valuation as
-adic valuation as  , so it remains to show that the first term is in
, so it remains to show that the first term is in 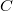 . Indeed, by assumption that
. Indeed, by assumption that  we have
we have  and thus
and thus 
Finally, one can show that  (key fact:
(key fact:  , where
, where  is a
is a  -adic unit).
¡õ
-adic unit).
¡õ
 be a bounded prism. Let
be a bounded prism. Let 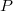 be a free
be a free  -algebra over
-algebra over  . Let
. Let  that form a regular sequence mod
that form a regular sequence mod  . Let
. Let  .
.
- The derived
 -completion
-completion  of
of  is
is  -completely flat over
-completely flat over  .
.  (the prismatic envelope; so in this case one can avoid transfinite construction in Lemma 19).
(the prismatic envelope; so in this case one can avoid transfinite construction in Lemma 19).
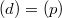 , reduce to the previous lemma. In general, do a base change argument.
¡õ
, reduce to the previous lemma. In general, do a base change argument.
¡õ
10/29/2018
 Crystalline comparison for prismatic cohomology
Crystalline comparison for prismatic cohomology
Let  be a
be a  -torsionfree
-torsionfree  complete
complete  -ring. Then
-ring. Then  is a bounded prism. Let
is a bounded prism. Let  be a smooth
be a smooth 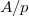 -algebra.
-algebra.
 of commutative algebra objects in
of commutative algebra objects in 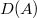 , compatible with the Frobenius action on both sides.
, compatible with the Frobenius action on both sides.
Let us explain why there is a canonical morphism from LHS to RHS.
Choose a free  -ring
-ring  together with a surjection
together with a surjection  . Recall that by definition
. Recall that by definition  . Since
. Since 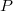 is now chosen to have a
is now chosen to have a  -structure, we know that
-structure, we know that 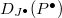 is a cosimplicial
is a cosimplicial  -algebra over
-algebra over  . On the other hand, the kernel
. On the other hand, the kernel  of
of  has divided powers. Consequently, we have
has divided powers. Consequently, we have  This the key relation between the
This the key relation between the  -structure and divided power structure and gives a commutative diagram
-structure and divided power structure and gives a commutative diagram ![$$\xymatrix{D_{J^\bullet}(P^\bullet) \ar@{->>}[d] \ar[r]^\phi & D_{J^\bullet}(P^\bullet) \ar@{->>}[d] \\ R=D_{J^\bullet}(P^\bullet)/K^\bullet \ar[r] & D_{J^\bullet}(P^\bullet)/p}$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_227344136_.gif) Notice that the lower right part of the diagram gives a cosimplicial object in the prismatic site
Notice that the lower right part of the diagram gives a cosimplicial object in the prismatic site 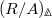 . Thus we obtain a canonical map
. Thus we obtain a canonical map  So by adjunction we obtain a map
So by adjunction we obtain a map  One can check this is an equivalence by explicitly computing both sides using Cech-Alexander complexes and using Lemma 20 to identify
One can check this is an equivalence by explicitly computing both sides using Cech-Alexander complexes and using Lemma 20 to identify  -structures and divided powers structures.
-structures and divided powers structures.
 Hodge-Tate comparison
Hodge-Tate comparison
Let  be a bounded prism. Let
be a bounded prism. Let  be a formally smooth
be a formally smooth 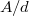 -algebra. Now let us sketch a proof of the Hodge-Tate comparison (Theorem 6).
-algebra. Now let us sketch a proof of the Hodge-Tate comparison (Theorem 6).
- Deduce the Hodge-Tate comparison from the crystalline comparison (Theorem 9) and the Cartier isomorphism (Theorem 8) when
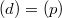 (and worry about the Frobenius twist when
(and worry about the Frobenius twist when 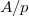 is not perfect).
is not perfect). - In general, set
 . Then the irreducibility lemma for distinguished elements (Lemma 10) implies that
. Then the irreducibility lemma for distinguished elements (Lemma 10) implies that 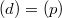 in
in 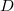 . We look at the base change along
. We look at the base change along  . Using Lemma 20, we may deduce the theorem from the previous case
. Using Lemma 20, we may deduce the theorem from the previous case 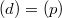 .
.
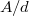 -scheme
-scheme 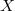 , one can define its prismatic cohomology
, one can define its prismatic cohomology 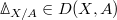 , compatible with passing to affine open subsets
, compatible with passing to affine open subsets 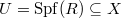 (i.e.,
(i.e., 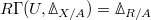 ).
).
 is a sheaf, it suffices to check it is a sheaf modulo
is a sheaf, it suffices to check it is a sheaf modulo 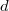 , which is true by identifying with differential forms via the Hodge-Tate comparison.
, which is true by identifying with differential forms via the Hodge-Tate comparison.
 Extension to the singular case
Extension to the singular case
 Non-abelian derived functors
Non-abelian derived functors
Our next goal is to explain how to extend the prismatic cohomology to the singular case. We will need to derive the functor of Kahler differentials, which is a functor from rings to modules. Since the category of rings is not abelian, we need some formalisms on non-abelian derived functors.
Let  be a commutative ring. Let
be a commutative ring. Let  be the category of finitely generated polynomial
be the category of finitely generated polynomial  -algebras. Consider a functor
-algebras. Consider a functor  e.g.,
e.g.,  . To derive
. To derive  , we view
, we view  as "projective" objects in
as "projective" objects in  .
.
 such that
such that
 commutes with filtered colimits.
commutes with filtered colimits. commutes with geometric realizations, i.e., if
commutes with geometric realizations, i.e., if  is a simplicial resolution of
is a simplicial resolution of  in
in  , then
, then  .
.
- Here
 is treated as an
is treated as an  -category.
-category.  is the homotopy colimit of
is the homotopy colimit of  , i.e., the direct sum totalization of the associated bicomplex.
, i.e., the direct sum totalization of the associated bicomplex.- There exists a canonical choice of a simplicial resolution
 such that each
such that each  is a (possibly not finitely generated) polynomial
is a (possibly not finitely generated) polynomial  -algebra:
-algebra: ![$$P_0=A[B], P_1=A[A[B]],\ldots,$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_190065451_.gif) (this is good for functoriality issues, but not so useful for explicit computation).
(this is good for functoriality issues, but not so useful for explicit computation).
 Cotangent complexes
Cotangent complexes
 .
.- If
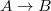 is smooth, then
is smooth, then ![$L_{B/A}=\Omega_{B/A}^1[0]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_244853545_-8.gif) .
. - (Transitivity triangle). For a composition
 , we have an extra triangle
, we have an extra triangle 
- If
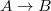 is surjective with kernel
is surjective with kernel 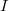 , then
, then  and
and  . Moreover, the other
. Moreover, the other  vanishes if
vanishes if 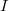 is generated by a regular sequence. This will be sufficient for most explicit computation we will encounter.
is generated by a regular sequence. This will be sufficient for most explicit computation we will encounter. - If
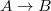 is a local complete intersection, then
is a local complete intersection, then  is concentrated in two degrees given by
is concentrated in two degrees given by  and
and  . If
. If 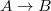 is not a local complete intersection, then
is not a local complete intersection, then  is unbounded (a conjecture of Quillen, proved by Avramov).
is unbounded (a conjecture of Quillen, proved by Avramov).
 Derived de Rham cohomology
Derived de Rham cohomology
Fix a ground ring 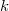 of characteristic
of characteristic  .
.
In char 0, for an affine space the functor  is a constant functor so there is no higher derived de Rham cohomology. But in char
is a constant functor so there is no higher derived de Rham cohomology. But in char  , even for an affine space
, even for an affine space  has a lot of cohomologies (given by the Cartier isomorphism). The following property helps us to control the derived de Rham cohomology.
has a lot of cohomologies (given by the Cartier isomorphism). The following property helps us to control the derived de Rham cohomology.
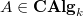 , there exists an increasing exhaustive filtration (conjugate filtration)
, there exists an increasing exhaustive filtration (conjugate filtration) 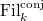 on
on 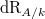 equipped with canonical isomorphisms
equipped with canonical isomorphisms ![$$\mathrm{gr}_i^\mathrm{conj}(\mathrm{dR}_{A/k})\cong \wedge^i L_{A^{(i)}/k}[-i],$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_9702711_.gif) where
where 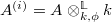 . More precisely, we have a lift of
. More precisely, we have a lift of 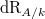 into the filtered derived category
into the filtered derived category 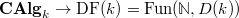 .
.
11/12/2018
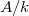 smooth, we have
smooth, we have 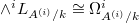 .
¡õ
.
¡õ
The moral here is that if we have a functor whose cohomology can be described in terms of differential forms, then its derived functor should also has a description in terms of differential forms. We will realize this idea for prismatic cohomology as well.
 Derived prismatic cohomology
Derived prismatic cohomology
Let 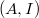 be a bounded prism. Let
be a bounded prism. Let  be a formally smooth
be a formally smooth 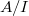 -algebra. We constructed the prismatic cohomology
-algebra. We constructed the prismatic cohomology  together with an action of the Frobenius
together with an action of the Frobenius 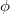 . Moreover, we have the Hodge-Tate comparison
. Moreover, we have the Hodge-Tate comparison 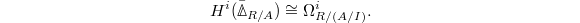
 is obtained by deriving
is obtained by deriving 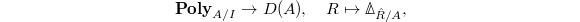 where
where  is the
is the  -adic completion of
-adic completion of  , and
, and  is the derived category of
is the derived category of 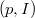 -complete
-complete  -complexes. Define
-complexes. Define  which is the same as the derived functor of
which is the same as the derived functor of 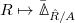 (as the non-abelian derived functor commutes with filtered colimits, in particular with
(as the non-abelian derived functor commutes with filtered colimits, in particular with 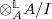 ).
).
One can check that  if
if  is the
is the  -adic completion of a polynomial
-adic completion of a polynomial 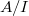 -algebra. We have the following derived version of the Hodge-Tate comparison.
-algebra. We have the following derived version of the Hodge-Tate comparison.
From now on by abuse of notation we will write  .
.
 Perfections in mixed characteristic
Perfections in mixed characteristic
Let 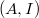 be a perfect prism (e.g.,
be a perfect prism (e.g., ![$(\mathbb{Z}_p[q^{1/p^\infty}]_{(p,q-1)}^\wedge,([p]_q))$](./latex/BhattEilenberg/latex2png-BhattEilenberg_131030896_-8.gif) , where
, where  ). Let
). Let  be a
be a  -complete
-complete 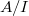 -algebra. Our next goal is to construct a "perfectoidization"
-algebra. Our next goal is to construct a "perfectoidization"  of
of  . It may not be perfectoid, but better be thought of as a "derived perfectoid ring". We will realize this using the prismatic cohomology of
. It may not be perfectoid, but better be thought of as a "derived perfectoid ring". We will realize this using the prismatic cohomology of  .
.
First let us look at the case of characteristic  , where we already know what
, where we already know what  should be.
should be.
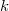 be a perfect field of characteristic
be a perfect field of characteristic  . For any
. For any 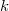 -algebra
-algebra  , define
, define 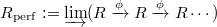 . The map
. The map 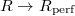 is the universal map from
is the universal map from  to a perfect
to a perfect  -algebra.
-algebra.
 be a
be a  -algebra, the prefection of the derived de Rham cohomology
-algebra, the prefection of the derived de Rham cohomology  (where
(where 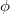 is induced by the Frobenius on
is induced by the Frobenius on  ) identifies with
) identifies with 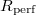 via the projection
via the projection 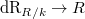 .
.
 = a polynomial
= a polynomial 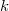 -algebra, and use
-algebra, and use 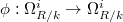 is zero for any
is zero for any  .
¡õ
.
¡õ
Now we can do the same thing for prismatic cohomology.
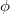 kills
kills ![$\mathrm{gr}_i^\mathrm{HT}(\bar \Delta_{R/A})=\wedge^iL_{R/k}[-i]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_259905092_-6.gif) . There is an extra subtlety: the Frobenius for the prismatic cohomology comes from the objects on
. There is an extra subtlety: the Frobenius for the prismatic cohomology comes from the objects on 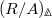 , while the Frobenius on differential forms comes from the ring
, while the Frobenius on differential forms comes from the ring  in characteristic
in characteristic  . Nevertheless one can check they are the same.
¡õ
. Nevertheless one can check they are the same.
¡õ
Now let us come to the mixed characteristic case. Let 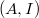 be a perfect prism. Let
be a perfect prism. Let  be an
be an 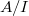 -algebra. We use the prismatic cohomology to define the perfectoidization of
-algebra. We use the prismatic cohomology to define the perfectoidization of  .
.
 is a commutative algebra object, and
is a commutative algebra object, and 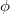 is an isomorphism on it.
is an isomorphism on it. is a commutative algebra object.
is a commutative algebra object.
- If
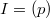 , then
, then  .
. - If
 is already perfectoid (e.g.,
is already perfectoid (e.g., 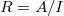 ), then
), then  (check:
(check:  , the unique lift of
, the unique lift of  from
from 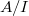 to
to  ).
). - Let
![$(A,I)=(\mathbb{Z}_p[q^{1/p^\infty}]_{(p,q-1)}^\wedge, ([p]_q))$](./latex/BhattEilenberg/latex2png-BhattEilenberg_246170741_-8.gif) . Let
. Let ![$R=A/I[X^{\pm1}]^\wedge$](./latex/BhattEilenberg/latex2png-BhattEilenberg_57953001_-5.gif) (a torus). We use the fact that (more on this later)
(a torus). We use the fact that (more on this later) ![$$\Delta_{R/A}=A[X^{\pm1}]^\wedge \xrightarrow{\nabla_q} A[X^{\pm1}]^\wedge dx/x,\quad \nabla_q(f(x))=\frac{f(qx)-f(x)}{q-1} dx/x.$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_49603548_.gif) Then one can compute that
Then one can compute that ![$$\Delta_{R/A,\mathrm{perf}}=A[X^{\pm 1/p^\infty}]^\wedge\xrightarrow{\gamma-1} J \cdot A[X^{\pm 1/p^\infty}]^\wedge,$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_150703343_.gif) where
where  and
and  for any
for any ![$i\in \mathbb{Z}[1/p]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_132684682_-5.gif) . Notice that when specializing to
. Notice that when specializing to 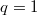 the term in degree one of this two-term complex is zero and we obtain a complex with one term. However, note that the element
the term in degree one of this two-term complex is zero and we obtain a complex with one term. However, note that the element  (= the image of
(= the image of 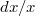 ) in degree one is not a co-boundary, and also nonzero in
) in degree one is not a co-boundary, and also nonzero in  (= nonzero mod
(= nonzero mod ![$[p]_q$](./latex/BhattEilenberg/latex2png-BhattEilenberg_54228657_-5.gif) ). Therefore
). Therefore  is genuinely derived (with nontrivial higher cohomology).
is genuinely derived (with nontrivial higher cohomology).
11/19/2018
![$(A,I)=(\mathbb{Z}_p[q^{1/p^\infty}]_{(p,q-1)}^\wedge,([p]_q))$](./latex/BhattEilenberg/latex2png-BhattEilenberg_118803715_-8.gif) .
.![$(A,I)=(\mathbb{Z}_p[u^{1/p^\infty}]^\wedge_{(p,u)}, (p-u))$](./latex/BhattEilenberg/latex2png-BhattEilenberg_210108664_-8.gif) (especially for etale comparison).
(especially for etale comparison).
 (there is no cohomology in negative degree; reason: power operation in homotopy theory).
(there is no cohomology in negative degree; reason: power operation in homotopy theory).- If
 (i.e., in degree 0), then
(i.e., in degree 0), then  is a perfect prism, and
is a perfect prism, and  is a perfectoid ring.
is a perfectoid ring.  is independent of the choice of
is independent of the choice of 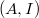 .
.- The functor
 commutes with faithfully flat base change
commutes with faithfully flat base change  .
.
As an application, we now reprove one of the key lemmas in André's recent breakthrough on the direct summand conjecture.
 be a perfectoid ring. Let
be a perfectoid ring. Let 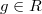 . Then there exists
. Then there exists  -completely faithfully flat map
-completely faithfully flat map  of perfectoid rings such that
of perfectoid rings such that  has a compatible system of
has a compatible system of  -power roots
-power roots 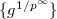 in
in 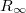 .
.
![$R=\mathbb{Z}_p[p^{1/p^\infty}]^\wedge$](./latex/BhattEilenberg/latex2png-BhattEilenberg_102420184_-5.gif) ,
,  . Notice that there are no
. Notice that there are no  -power roots of
-power roots of  in
in  . Andre's proof used the full power of the theory of perfectoid spaces and in particular the tilting equivalence.
. Andre's proof used the full power of the theory of perfectoid spaces and in particular the tilting equivalence.
 be the perfect prism corresponds to
be the perfect prism corresponds to  . Let
. Let 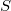 be the
be the  -adic completion of
-adic completion of ![$R[X^{1/p^\infty}]/(x-g)$](./latex/BhattEilenberg/latex2png-BhattEilenberg_175677507_-5.gif) . Then
. Then  is
is  -completely faithfully flat. We claim that taking
-completely faithfully flat. We claim that taking  solves the problem: i.e.,
solves the problem: i.e., 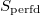 is perfectoid and
is perfectoid and  is
is  -completely faithfully flat. It suffices to show the latter is true (as faithfully flat implies living in only degree 0). Equivalently, we need to show that
-completely faithfully flat. It suffices to show the latter is true (as faithfully flat implies living in only degree 0). Equivalently, we need to show that  is
is 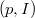 -completely faithfully flat.
-completely faithfully flat.
Now it suffices to show that each individual term  in the perfection is
in the perfection is 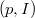 -completely faithfully flat over
-completely faithfully flat over  (use the stability of faithfully flatness for
(use the stability of faithfully flatness for  , and use
, and use  is perfect to change the twisted
is perfect to change the twisted  -module to
-module to  -module structure), which is equivalent to showing that
-module structure), which is equivalent to showing that  is
is  -completely faithfully flat.
-completely faithfully flat.
By the Hodge-Tate comparison, it suffices to show that each graded piece ![$\wedge^iL_{S/R}[-i]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_82369473_-6.gif) is
is  -completely faithfully flat. Since
-completely faithfully flat. Since ![$L_{R[X^{1/p^\infty}]/R}$](./latex/BhattEilenberg/latex2png-BhattEilenberg_95919107_-7.gif) is
is  -adically zero (divisible by any
-adically zero (divisible by any  -power), we know that
-power), we know that ![$$L_{S/R}\cong L_{S/R[X^{1/p^\infty}]}=S[ 1 ],$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_17211576_.gif) as
as  is a nonzerodivisor. So
is a nonzerodivisor. So ![$$\wedge^0L_{S/R}[ 0 ]=S, \wedge^1L_{S/R}[- 1 ]\cong S,\cdots, \wedge^nL_{S/R}[-n]\cong \Gamma_{S}^n(S)\cong S.$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_71826156_.gif) (
( is the degree
is the degree  divided power polynomials of
divided power polynomials of 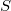 ). Each graded piece is a free module of rank 1 in degree zero, hence
). Each graded piece is a free module of rank 1 in degree zero, hence  -complete faithfully flat.
¡õ
-complete faithfully flat.
¡õ
 be a perfectoid ring and
be a perfectoid ring and 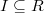 an ideal. Let
an ideal. Let 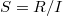 . Then
. Then 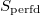 lives in degree 0, and
lives in degree 0, and 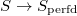 is surjective.
is surjective.
 ) are the same.
) are the same.
![$R_0=\mathbb{Z}_p^\mathrm{cyc}=\mathbb{Z}_p[q^{1/p^\infty}]/([p]_q)^\wedge$](./latex/BhattEilenberg/latex2png-BhattEilenberg_58875941_-6.gif) . Let
. Let ![$R=R_0[X^{1/p^\infty}]^\wedge$](./latex/BhattEilenberg/latex2png-BhattEilenberg_140200332_-5.gif) and
and  . I don't know how to describe
. I don't know how to describe 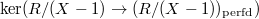 explicitly (or even write down a nontrivial element in the kernel explicitly).
explicitly (or even write down a nontrivial element in the kernel explicitly).
 The etale comparison
The etale comparison
Let 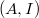 be a perfect prism. Let
be a perfect prism. Let  be a
be a  -complete
-complete 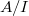 -algebra. Assume
-algebra. Assume  is finitely generated over
is finitely generated over 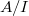 and
and ![$R[p^\infty]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_158184558_-5.gif) is bounded.
is bounded.
Our next goal is to prove Theorem 11. To simplify notation, assume 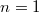 . The main steps are:
. The main steps are:
- Reduce from
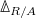 to
to  (most interesting step).
(most interesting step). - Reduce to
 semiperfectoid (quotient of perfectoid; its prismatic cohomology lives in degree 0).
semiperfectoid (quotient of perfectoid; its prismatic cohomology lives in degree 0). - Reduce to
 perfectoid (for which the theorem was known before: dates back to e.g. Fontaine-Wintenberger in 70's).
perfectoid (for which the theorem was known before: dates back to e.g. Fontaine-Wintenberger in 70's).
Step (a) A continuity property inspired by topological cyclic homology.
 be an
be an 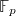 -algebra and
-algebra and 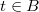 . Define the category of Frobenius modules
. Define the category of Frobenius modules ![$$D(B[F])=\{(M, \phi_M): M\in D(B), \phi_M: M\rightarrow\phi_*M\},$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_26056190_.gif) and a subcategory
and a subcategory ![$D_\mathrm{comp}(B[F])$](./latex/BhattEilenberg/latex2png-BhattEilenberg_62696626_-5.gif) such that
such that  is
is  -complete. The colimits in
-complete. The colimits in ![$D_\mathrm{comp}(B[F])$](./latex/BhattEilenberg/latex2png-BhattEilenberg_62696626_-5.gif) are computed by the
are computed by the  -completion of the usual colimit.
-completion of the usual colimit.
- The fixed point functor
![$$(\cdot)^{\phi=1}: D(B[F])\rightarrow D(\mathbb{F}_p),\quad (M,\phi)\mapsto M^{\phi=1}:=\mathrm{fib}(M\xrightarrow{\phi-1}M)$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_259778660_.gif) commutes with colimits.
commutes with colimits. - The fixed point functor
![$$D_\mathrm{comp}(B[F])\rightarrow D(\mathbb{F}_p),\quad (M,\phi)\mapsto M[1/t]^{\phi=1}$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_92220440_.gif) commutes with colimits.
commutes with colimits. - Let
![$(M,\phi)\in D_\mathrm{comp}(B[F])$](./latex/BhattEilenberg/latex2png-BhattEilenberg_44083995_-5.gif) , then the perfection
, then the perfection  induces an isomorphism on
induces an isomorphism on  .
.
 be a diagram in
be a diagram in ![$D_\mathrm{comp}(B[F])$](./latex/BhattEilenberg/latex2png-BhattEilenberg_62696626_-5.gif) . We have a commutative diagram
. We have a commutative diagram ![$$\xymatrix{\colim M_i \ar[r]^a \ar[d]& (\colim M_i)^\wedge \ar[d] \\ \colim M_i[1/t] \ar[r]^b & (\colim M_i)^\wedge[1/t].}$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_19336993_.gif) Then (a) is equivalent to
Then (a) is equivalent to  , and (b) is equivalent to
, and (b) is equivalent to  . As
. As  is uniquely
is uniquely  -divisible, we know that
-divisible, we know that  . Therefore it suffices to show that
. Therefore it suffices to show that  , or equivalently,
, or equivalently,  commutes with colimits.
commutes with colimits.
We claim that for any ![$(N,\phi)\in D_\mathrm{comp}(B[F])$](./latex/BhattEilenberg/latex2png-BhattEilenberg_44088091_-5.gif) ,
,  induces an isomorphism on
induces an isomorphism on  (then the result follows since
(then the result follows since  commutes with colimits before completion). To prove the claim, notice that
commutes with colimits before completion). To prove the claim, notice that  has a complete descending filtration
has a complete descending filtration  such that
such that 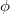 is topological nilpotent on the filtration:
is topological nilpotent on the filtration:  (think: Frobenius is contracting). Thus
(think: Frobenius is contracting). Thus  is an isomorphism on
is an isomorphism on  .
¡õ
.
¡õ
The upshot is that to prove the Theorem 11, it suffices to show the same thing for ![$(\Delta_{R/A,\mathrm{perf}}[1/d]/p^n)^{\phi=1}$](./latex/BhattEilenberg/latex2png-BhattEilenberg_130739385_-6.gif) (after the perfection).
(after the perfection).
Step (b) Let ![$T=A/I[X_1, \ldots, X_n]^\wedge$](./latex/BhattEilenberg/latex2png-BhattEilenberg_220367677_-5.gif) be a polynomial algebra. We take the perfectoid ring
be a polynomial algebra. We take the perfectoid ring ![$T_\infty=A/I[X_1^{1/p^\infty}, \ldots, X_n^{1/p^\infty}]^\wedge$](./latex/BhattEilenberg/latex2png-BhattEilenberg_83594616_-5.gif) . We have a faithfully flat map
. We have a faithfully flat map  . Let
. Let  be the Cech nerve of
be the Cech nerve of  (i.e.,
(i.e.,  ). Then each
). Then each  is semiperfectoid.
is semiperfectoid.
For more general  , choose topological generators
, choose topological generators  to get a surjective map
to get a surjective map  . Repeating the previous construction we obtain
. Repeating the previous construction we obtain  , where each
, where each  is semiperfectoid.
is semiperfectoid.
Now the strategy is to reduce Theorem 11 for  to the same thing for
to the same thing for  .
.
- (descent for etale cohomology)
![$$R\Gamma(\Spec R[1/p], \mathbb{F}_p)\cong\varprojlim R\Gamma(\Spec R_\infty^*[1/p], \mathbb{F}_p).$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_83391470_.gif) (true for any torsion contractible sheaves).
(true for any torsion contractible sheaves). - (descent for prismatic cohomology)
![$$(\Delta_{R/A}[1/d]/p)^{\phi=1}\cong\varprojlim(\Delta_{R_\infty^*/A}[1/d]/p)^{\phi=1}$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_130983920_.gif) and the same for
and the same for  and
and ![$\Delta_{\cdot/A,\mathrm{perf}}[1/d]/p$](./latex/BhattEilenberg/latex2png-BhattEilenberg_20367326_-6.gif) (the proof uses tools developed in Akhil Mathew's undergraduate thesis).
(the proof uses tools developed in Akhil Mathew's undergraduate thesis).
11/26/2018
Step (c) Let  be semiperfectoid and
be semiperfectoid and  be its perfectoidization. By Corollary 11, we know that
be its perfectoidization. By Corollary 11, we know that  lives in degree 0 and hence is perfectoid. We claim that both sides of the desired isomorphism
lives in degree 0 and hence is perfectoid. We claim that both sides of the desired isomorphism ![$$R\Gamma_\mathrm{et}(\Spec R[1/p], \mathbb{Z}/p^n)\cong (\Delta_{R/A, \mathrm{perf}}[1/d]/p^n)^{\phi=1}$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_133464801_.gif) do not change when replacing
do not change when replacing  by
by  . For the RHS, we claim that
. For the RHS, we claim that  In fact both reduce to
In fact both reduce to  mod
mod 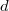 (by the Hodge-Tate comparison and the definition of
(by the Hodge-Tate comparison and the definition of  ), and hence the claim is true by the derived completeness of both. For the LHS, one shows that
), and hence the claim is true by the derived completeness of both. For the LHS, one shows that  induces an isomorphism of associated
induces an isomorphism of associated  -sheaves (which we have not covered) and one gets (by a theorem) that they have the same etale cohomology for the generic fiber.
-sheaves (which we have not covered) and one gets (by a theorem) that they have the same etale cohomology for the generic fiber.
Therefore it remains to prove the etale comparison when  is perfectoid. In this case, by a (classical) theorem, we have
is perfectoid. In this case, by a (classical) theorem, we have ![$$R\Gamma_\mathrm{et}(\Spec R[1/p], \mathbb{F}_p)\cong R^\flat[1/d]^{\phi=1}.$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_43461207_.gif) (in modern terminology, this can be proved using the pro-etale site of perfectoid spaces and the exactness of the Artin-Schreier sequence). Since
(in modern terminology, this can be proved using the pro-etale site of perfectoid spaces and the exactness of the Artin-Schreier sequence). Since  is perfectoid, we have
is perfectoid, we have  and hence
and hence ![$\Delta_{R/A}[1/d]/p\cong R^\flat[1/d]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_44046709_-6.gif) . Thus we have proved the etale comparison when
. Thus we have proved the etale comparison when  is perfectoid.
is perfectoid.
In particular, the 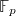 -etale cohomology of
-etale cohomology of ![$\Spec R[1/p]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_73381446_-5.gif) lives in only two degrees (in fact, by the same etale comparison theorem with nontrivial coefficient systems, one can show that
lives in only two degrees (in fact, by the same etale comparison theorem with nontrivial coefficient systems, one can show that ![$\Spec R[1/p]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_73381446_-5.gif) is a
is a  ).
).
Now let us come back to prove our main application.
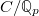 be complete and algebraically closed. Let
be complete and algebraically closed. Let 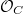 be the valuation ring (which is perfectoid) with residue field
be the valuation ring (which is perfectoid) with residue field 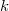 . Let
. Let 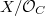 be a proper smooth formal scheme. Then
be a proper smooth formal scheme. Then 
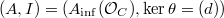 be the perfect prism associated to
be the perfect prism associated to 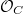 . So
. So 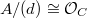 . The map
. The map  induces a map
induces a map 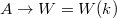 , and a map of perfect prisms
, and a map of perfect prisms 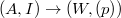 . The prismatic complex
. The prismatic complex 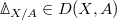 is obtained by gluing
is obtained by gluing 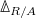 for all open
for all open 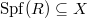 . Similarly, we have the prismatic complex
. Similarly, we have the prismatic complex 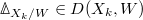 . We have an base change isomorphism (by the Hodge-Tate comparison)
. We have an base change isomorphism (by the Hodge-Tate comparison) 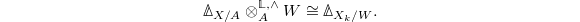 (Notice that since
(Notice that since  is a formal scheme,
is a formal scheme, 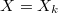 as topological spaces and we can identify sheaves on them).
as topological spaces and we can identify sheaves on them).
Let  , and similarly define
, and similarly define  . We claim that
. We claim that  is a perfect complex, i.e., represented by a finite complex of finite free modules. To prove the claim, it suffices to show that
is a perfect complex, i.e., represented by a finite complex of finite free modules. To prove the claim, it suffices to show that  . This is true by the Hodge-Tate comparison:
. This is true by the Hodge-Tate comparison:  has a filtration whose graded pieces are given by
has a filtration whose graded pieces are given by ![$R\Gamma(X, \Omega_{X/\mathcal{O}_C}^i)[-i]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_187716085_-8.gif) , which is perfect since
, which is perfect since  is proper and smooth.
is proper and smooth.
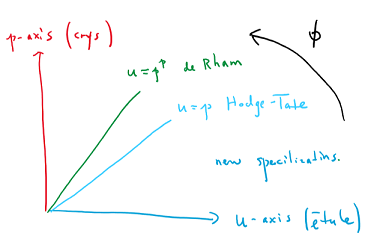
Let  with fraction field
with fraction field  and residue field
and residue field 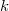 . Then by the semicontinuity for finitely presented
. Then by the semicontinuity for finitely presented  -modules, we obtain
-modules, we obtain 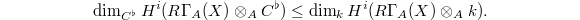
The RHS is given by  which is given by (the Frobenius of twist)
which is given by (the Frobenius of twist)  by the crystalline comparison for prismatic cohomology.
by the crystalline comparison for prismatic cohomology.
For the LHS: by the etale comparison we obtain  We then apply the following linear algebra lemma to
We then apply the following linear algebra lemma to  to get the desired inequality. (In fact, using the
to get the desired inequality. (In fact, using the  -de Rham complex, we will see that
-de Rham complex, we will see that 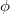 is an isomorphism for
is an isomorphism for  and hence the dimension of the LHS is equal to the dimension of
and hence the dimension of the LHS is equal to the dimension of 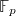 -etale cohomology of the generic fiber
-etale cohomology of the generic fiber  ).
¡õ
).
¡õ
 be an algebraically closed field of characteristic
be an algebraically closed field of characteristic  . Let
. Let 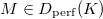 and
and 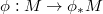 . Then
. Then  is injective, and moreover an isomorphism when
is injective, and moreover an isomorphism when 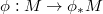 is an isomorphism.
is an isomorphism.
 The
The  -de Rham complex
-de Rham complex
As an analogue of crystalline cohomology being the de Rham cohomology of a lift, we would like to compute 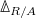 on the nose (as a genuine complex).
on the nose (as a genuine complex).
We will work with ![$\mathbb{Z}_p[ [q-1]]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_189630513_-5.gif) with
with  , and
, and ![$d=[p]_q=\frac{q^p-1}{q-1}$](./latex/BhattEilenberg/latex2png-BhattEilenberg_12396435_-8.gif) . Let
. Let ![$\mathbb{Z}_p[\varepsilon]=\mathbb{Z}_p[ [q-1]]/[p]_q$](./latex/BhattEilenberg/latex2png-BhattEilenberg_248223118_-5.gif) .
.
![$R=\mathbb{Z}_p[x]^\wedge$](./latex/BhattEilenberg/latex2png-BhattEilenberg_245171241_-5.gif) . We define its
. We define its  -de Rham complex (depending on the choice of
-de Rham complex (depending on the choice of  )
) ![$$q\Omega_{R, \square}^*:=R[ [q-1]]\xrightarrow{\nabla_q}R[ [q-1]]dx,$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_112834088_.gif) where we define the
where we define the ![$\mathbb{Z}_p[ [q-1]]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_189630513_-5.gif) -linear map
-linear map  Notice that the definition makes sense since
Notice that the definition makes sense since 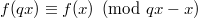 . Notice that
. Notice that ![$\nabla_q(x^n)=[n]_q x^{n-1}dx$](./latex/BhattEilenberg/latex2png-BhattEilenberg_64868803_-5.gif) . Therefore
. Therefore  on the nose. We have a similar construction for
on the nose. We have a similar construction for ![$R=\mathbb{Z}_p[x_1,\ldots,x_n]^\wedge$](./latex/BhattEilenberg/latex2png-BhattEilenberg_146119435_-5.gif) .
.
 satisfies the
satisfies the  -Leibniz rule
-Leibniz rule  This means that we may make
This means that we may make 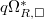 a dga by making
a dga by making  a
a  -bimodule via
-bimodule via  Notice that this dga is not commutative. Nevertheless, it turns out to be commutative up to all possible homotopies (an
Notice that this dga is not commutative. Nevertheless, it turns out to be commutative up to all possible homotopies (an  -algebra).
-algebra).
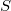 be a formally smooth
be a formally smooth 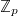 -algebra. A framing of
-algebra. A framing of 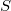 is a formally etale map
is a formally etale map ![$$\square: \mathbb{Z}_p[x_1, \ldots, x_n]^\wedge\rightarrow S.$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_161459851_.gif) We call such
We call such 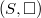 a framed pair.
a framed pair.
 -de Rham complex for framed pairs)
Let
-de Rham complex for framed pairs)
Let 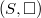 be a framed pair. We obtain a formally etale map
be a framed pair. We obtain a formally etale map ![$$\tilde\square: \mathbb{Z}[q-1, x_1,\ldots,x_n]^\wedge\rightarrow S[ [q-1]]$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_36424969_.gif) of
of ![$\mathbb{Z}_p[ [q-1]]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_189630513_-5.gif) -algebras. For
-algebras. For 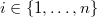 , we have an automorphism
, we have an automorphism 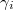 of
of ![$\mathbb{Z}_p[q-1,x_1,\ldots,x_n]^\wedge$](./latex/BhattEilenberg/latex2png-BhattEilenberg_202778071_-5.gif) such that
such that 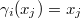 if
if 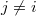 and
and 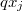 if
if 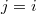 . Since
. Since 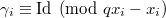 , we obtain a unique automorphism
, we obtain a unique automorphism 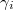 of
of ![$S[ [q-1]]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_164121102_-5.gif) extending it (by the formal smoothness of
extending it (by the formal smoothness of 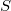 ). We define
). We define 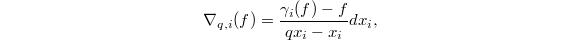 and the
and the  -de Rham complex to be the Koszul complex
-de Rham complex to be the Koszul complex ![$$q\Omega_{S,\square}^*=\mathrm{Kos}(S[ [q-1]]; \nabla_{q,1},\ldots,\nabla_{q,n})=(S[ [q-1]] \xrightarrow{\nabla_q} \oplus_{i=1}^n S[ [q-1]]dx_i\rightarrow\cdots ).$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_76928650_.gif)
12/03/2018
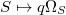 from formally smooth
from formally smooth 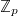 -algebras to
-algebras to ![$D_\mathrm{comp}(\mathbb{Z}_p[ [q-1]])$](./latex/BhattEilenberg/latex2png-BhattEilenberg_182152521_-5.gif) , equipped with natural isomorphisms
, equipped with natural isomorphisms  for each choice
for each choice  of framing. In particular,
of framing. In particular, 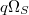 is a commutative algebra in
is a commutative algebra in ![$D_\mathrm{comp}(\mathbb{Z}_p[ [q-1]]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_145619460_-5.gif) , and each
, and each 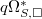 is an
is an  -algebra.
-algebra.
Our next goal is to prove Conjecture 1. It is hard to prove from first principle: it is already not clear how to write down the endomorphism of the  -de Rham complex for the simple change of variable
-de Rham complex for the simple change of variable  .
.
- Conjecture 1 is closely related to integral
 -adic Hodge theory, which proves the conjecture after base change along
-adic Hodge theory, which proves the conjecture after base change along ![$$\mathbb{Z}_p[ [q-1]]\rightarrow \mathbb{Z}_p[ [q^{1/p^\infty}]]_{(p,q-1)}^\wedge.$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_156229790_.gif) Thus Conjecture 1 can be thought of as a "de-perfection" of this statement.
Thus Conjecture 1 can be thought of as a "de-perfection" of this statement. - Conjecture 1 is easy after base change along
![$$\mathbb{Z}_p[ [q-1]]\rightarrow \mathbb{Q}_p[ [q-1]],$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_32821016_.gif) as the
as the  -de Rham complex is indeed isomorphic to the de Rham complex over
-de Rham complex is indeed isomorphic to the de Rham complex over ![$\mathbb{Q}_p[ [q-1]]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_78804944_-5.gif) (by Taylor expansion).
(by Taylor expansion). - Conjecture 1 still makes sense if we replace
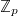 with any
with any  -complete ring, but it is not true in this generality. For example, it fails for
-complete ring, but it is not true in this generality. For example, it fails for 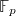 (as one cannot compute the
(as one cannot compute the 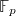 -etale cohomology of the generic fiber from the special fiber). We will see that the natural general context Conjecture 1 holds is provided by
-etale cohomology of the generic fiber from the special fiber). We will see that the natural general context Conjecture 1 holds is provided by  -PD thickenings.
-PD thickenings.
 The
The  -crystalline cohomology
-crystalline cohomology
Our goal is to construct a  -crystalline site
-crystalline site ![$(R/\mathbb{Z}_p[ [q-1]])_\mathrm{qcrys}$](./latex/BhattEilenberg/latex2png-BhattEilenberg_27693620_-5.gif) whose cohomology is computed by
whose cohomology is computed by  -de Rham complexes.
-de Rham complexes.
Write ![$A=\mathbb{Z}_p[ [q-1]]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_189640794_-5.gif) with
with  . Let
. Let  . Let
. Let ![$\mathbb{Z}_p[\varepsilon_p]:=A/([p]_q)$](./latex/BhattEilenberg/latex2png-BhattEilenberg_259493684_-5.gif) . Observe that the ideals
. Observe that the ideals  and
and ![$(p, [p]_q)$](./latex/BhattEilenberg/latex2png-BhattEilenberg_91858416_-5.gif) define the same topology (one is contained in the power of the other and vice versa).
define the same topology (one is contained in the power of the other and vice versa).
The main new ingredient is the notion of  -PD thickenings.
-PD thickenings.
 -PD pair
-PD pair 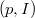 is a pair where
is a pair where 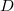 is a
is a  -algebra over
-algebra over  , and
, and  is an ideal such that
is an ideal such that
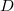 and
and  are
are ![$(p, [p]_q)$](./latex/BhattEilenberg/latex2png-BhattEilenberg_91858416_-5.gif) -complete.
-complete.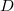 is
is ![$[p]_q$](./latex/BhattEilenberg/latex2png-BhattEilenberg_54228657_-5.gif) -torsionfree.
-torsionfree.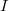 contains
contains  and
and ![$\phi(I)\subseteq [p]_q D$](./latex/BhattEilenberg/latex2png-BhattEilenberg_125624616_-5.gif) (the analogue of the PD-structure, see Lemma 20).
(the analogue of the PD-structure, see Lemma 20).
We call  the corresponding
the corresponding  -PD thickening. Conjecture 1 will be proved in this generality.
-PD thickening. Conjecture 1 will be proved in this generality.
 is a
is a  -PD pairing, and is the initial such pair. More generally for any
-PD pairing, and is the initial such pair. More generally for any ![$(p,[p]_q)$](./latex/BhattEilenberg/latex2png-BhattEilenberg_165140976_-5.gif) -completely flat
-completely flat  -algebra
-algebra 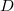 over
over  , we obtain a
, we obtain a  -PD pair
-PD pair  .
.- If
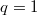 in
in  , then condition (c) is equivalent to that for any
, then condition (c) is equivalent to that for any  ,
,  for any
for any  (the usual PD-structure requires
(the usual PD-structure requires  , but it turns out to not affect anything).
, but it turns out to not affect anything).
 is
is  -flat. We would like to show that
-flat. We would like to show that ![$$\frac{\phi^2(f)}{\phi([p]_q)}\equiv\phi(\delta(f))\pmod{ [p]_qD}.$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_155857509_.gif) In
In ![$D/[p]_qD$](./latex/BhattEilenberg/latex2png-BhattEilenberg_201398000_-5.gif) , we have
, we have ![$\phi([p]_q)=\frac{q^{p^2}-1}{q^p-1}=p$](./latex/BhattEilenberg/latex2png-BhattEilenberg_261589281_-8.gif) (think:
(think: ![$[p]_q$](./latex/BhattEilenberg/latex2png-BhattEilenberg_54228657_-5.gif) and
and ![$\phi([p]_q)$](./latex/BhattEilenberg/latex2png-BhattEilenberg_192957934_-5.gif) are "transverse" to each other), so it suffices to show that
are "transverse" to each other), so it suffices to show that ![$$\phi^2(f)\equiv p \phi(\delta(f))\pmod{ [p]_qD}.$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_14703619_.gif) By definition,
By definition,  applying
applying 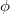 we obtain
we obtain  and
and ![$\phi(f)^p\in [p]_qD$](./latex/BhattEilenberg/latex2png-BhattEilenberg_44054050_-5.gif) by assumption.
¡õ
by assumption.
¡õ
 -PD envelopes)
Let
-PD envelopes)
Let  be a formally smooth
be a formally smooth 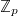 -algebra. Let
-algebra. Let 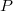 be formally smooth
be formally smooth  -algebra over
-algebra over  , equipped with a surjection
, equipped with a surjection  with kernel
with kernel 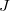 . There is a universal map
. There is a universal map  to a
to a  -PD pair. It has the following properties
-PD pair. It has the following properties
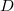 is
is ![$(p,[p]_q)$](./latex/BhattEilenberg/latex2png-BhattEilenberg_165140976_-5.gif) -completely flat over
-completely flat over  .
.- The map
 induces an isomorphism
induces an isomorphism  .
. - The map
 is the usual
is the usual  -completed PD-envelope of
-completed PD-envelope of  .
.
We denote  .
.
![$D=P\{\phi(x_1)/[p]_q,\ldots, \phi(x_n)/[p]_q\}^\wedge_{(p,q-1)}$](./latex/BhattEilenberg/latex2png-BhattEilenberg_109996662_-8.gif) , where
, where 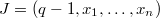 , and
, and 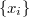 form a regular sequence.
¡õ
form a regular sequence.
¡õ
![$R=\mathbb{Z}_p[t]^\wedge$](./latex/BhattEilenberg/latex2png-BhattEilenberg_244909097_-5.gif) ,
, ![$P=A[x,y]^\wedge$](./latex/BhattEilenberg/latex2png-BhattEilenberg_213304260_-5.gif) , and
, and 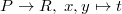 with
with  ,
,  . Then one can compute that
. Then one can compute that 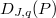 contains
contains ![$$\gamma_{k,q}(x-y)=\frac{(x-y)(x-qy)\cdots (x-q^{k-1}y)}{[ k]_q[ k-1]_q\cdots [ 1]_q}.$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_248566616_.gif) And they form a topological basis over
And they form a topological basis over ![$A[x]^\wedge$](./latex/BhattEilenberg/latex2png-BhattEilenberg_147478489_-5.gif) . (This was the motivating example for inventing the
. (This was the motivating example for inventing the  -crystalline site).
-crystalline site).
 -crystalline site)
Let
-crystalline site)
Let  be a formally smooth
be a formally smooth 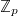 -algebra. Define
-algebra. Define 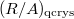 to be the category of
to be the category of  -PD pairs
-PD pairs  such that
such that 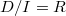 , and make it into a site via indiscrete topology (so presheaves=sheaves). Let
, and make it into a site via indiscrete topology (so presheaves=sheaves). Let 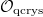 be the sheaf
be the sheaf 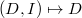 . Define the
. Define the  -crystalline cohomology to be
-crystalline cohomology to be 
To compute  , we use the Cech-Alexander complexes for
, we use the Cech-Alexander complexes for  (compare Theorem 7). Choose a surjection
(compare Theorem 7). Choose a surjection  with kernel
with kernel  such that
such that  is a
is a ![$(p,[p]_q)$](./latex/BhattEilenberg/latex2png-BhattEilenberg_165140976_-5.gif) -completion of a free
-completion of a free  -algebra over
-algebra over  . We obtain a cosimplicial
. We obtain a cosimplicial  -algebra over
-algebra over 
 with ideal
with ideal  such that
such that  . Taking
. Taking  -PD envelopes gives a cosimplicial object of
-PD envelopes gives a cosimplicial object of 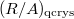 ,
,  Category theory (Lemma 18) then implies that
Category theory (Lemma 18) then implies that 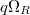 is given by
is given by  .
.
12/10/2018

 -crystalline comparison and
-crystalline comparison and  -de Rham comparison
-de Rham comparison
Let  be formally smooth over
be formally smooth over 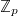 . Let
. Let ![$R^{(1)}:=R \otimes_{\mathbb{Z}_p}\mathbb{Z}_p[\varepsilon_p]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_154948029_-6.gif) . Notice that we have the following commutative diagram
. Notice that we have the following commutative diagram ![$$\xymatrix{A \ar[r]^{\phi_A} \ar[d] & A \ar[d] \ar@{=}[r] & A \ar[d] \\ \mathbb{Z}_p=A/(q-1) \ar[r] \ar[d] & A/(q^p-1) \ar[r] & A/([p]_q) \ar[d] \\ R \ar[rr]& & R^{(1)}.}$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_102072777_.gif) The left vertical column corresponds to the
The left vertical column corresponds to the  -crystalline cohomology, and the right vertical column corresponds to the prismatic cohomology. The twist
-crystalline cohomology, and the right vertical column corresponds to the prismatic cohomology. The twist 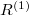 is needed as
is needed as  is not a distinguished element but
is not a distinguished element but ![$[p]_q$](./latex/BhattEilenberg/latex2png-BhattEilenberg_54228657_-5.gif) is.
is.
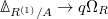 , we need to show that for each
, we need to show that for each 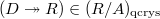 , we get an object
, we get an object ![$(R^{(1)}\rightarrow D/[p]_q\leftarrow D)\in (R^{(1)}/A)_\Delta$](./latex/BhattEilenberg/latex2png-BhattEilenberg_32101192_-5.gif) . By the definition of
. By the definition of  -PD thickening, we have a commutative diagram
-PD thickening, we have a commutative diagram ![$$\xymatrix{D \ar[r]^\phi \ar[d] & D \ar[d] \\ R \ar[r] & D/[p]_qD.}$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_177012325_.gif) Linearizing along
Linearizing along 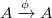 we obtain the desired object in the prismatic site. To check this map is an isomorphism, we check after
we obtain the desired object in the prismatic site. To check this map is an isomorphism, we check after 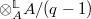 and use the crystalline comparison for prismatic cohomology.
¡õ
and use the crystalline comparison for prismatic cohomology.
¡õ
Our next goal is to relate 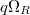 to
to 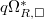 . In the classical characteristic
. In the classical characteristic  setting this relation is saying that the crystalline-de Rham comparison does not depend the choice of the lift. One can basically add
setting this relation is saying that the crystalline-de Rham comparison does not depend the choice of the lift. One can basically add  everywhere in the proof for the classical case, and it works.
everywhere in the proof for the classical case, and it works.
 -de Rham complexes for
-de Rham complexes for  -PD envelopes)
Let
-PD envelopes)
Let 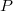 be a formally smooth
be a formally smooth  -algebra, formally etale over
-algebra, formally etale over ![$A[x_1,\ldots,x_n]^\wedge$](./latex/BhattEilenberg/latex2png-BhattEilenberg_144450709_-5.gif) (which is given a unique
(which is given a unique  -structure satisfying
-structure satisfying 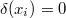 ). Assume there is a surjection
). Assume there is a surjection  and
and 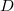 is the
is the  -PD envelope of
-PD envelope of  . By the following lemma, we can extend the
. By the following lemma, we can extend the  -de Rham complex
-de Rham complex 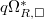 to
to 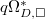 (from
(from 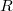 to
to 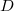 ).
).
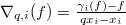 . It suffices to show that each
. It suffices to show that each  extends uniquely to an automorphism of
extends uniquely to an automorphism of  congruent to
congruent to 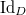 mod
mod 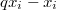 . Using the universal property of
. Using the universal property of 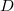 , we need to show that for each
, we need to show that for each 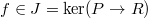 , we have
, we have ![$\phi(\gamma_i(f))\subseteq [p]_q D$](./latex/BhattEilenberg/latex2png-BhattEilenberg_17298432_-5.gif) and
and ![$$\frac{\phi(\gamma_i(f))}{[p]_q}\equiv\frac{\phi(f)}{[p]_q}\pmod{(qx_i-x_i)D}.$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_194366256_.gif) In fact,
In fact, 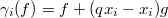 for some
for some  , and so
, and so 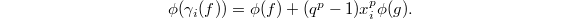 Dividing by
Dividing by ![$[p]_q$](./latex/BhattEilenberg/latex2png-BhattEilenberg_54228657_-5.gif) , we obtain the desired result.
¡õ
, we obtain the desired result.
¡õ
 -crystalline-de Rham comparison)
Let
-crystalline-de Rham comparison)
Let  be a framed
be a framed  -algebra. Then there exists a natural isomorphism
-algebra. Then there exists a natural isomorphism 
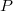 be the unique lift of
be the unique lift of  to
to  with coordinates
with coordinates 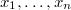 . Let
. Let 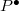 be the Cech nerve of
be the Cech nerve of 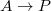 . We have a surjection
. We have a surjection  with kernel
with kernel  , and
, and 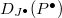 is a cosimplicial
is a cosimplicial  -algebra over
-algebra over  computing
computing  . To relate it to
. To relate it to  , we use the bicomplex
, we use the bicomplex 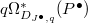 . Notice that
. Notice that 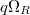 is computed by the first row of this bicomplex and
is computed by the first row of this bicomplex and 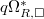 is computed by the first column of this bicomplex. To show they are quasi-isomorphic, we combine:
is computed by the first column of this bicomplex. To show they are quasi-isomorphic, we combine:
- All horizontal maps give quasi-isomorphisms of the columns (reduce mod
 and use the Poincare lemma: adding free variables does not change the cohomology). So the bicomplex totalizes to the first column.
and use the Poincare lemma: adding free variables does not change the cohomology). So the bicomplex totalizes to the first column. - All rows except first column are acyclic (write down explicit combinatorial contracting homotopy). So the bicomplex also totalizes to the first row. ¡õ
 -de Rham complex (with the explicit description of the Frobenius in coordinates) to show that
-de Rham complex (with the explicit description of the Frobenius in coordinates) to show that  is an isogeny (i.e., it has an inverse up to multiplication by
is an isogeny (i.e., it has an inverse up to multiplication by  , where
, where  ).
).
 Prismatic cohomology via topological Hochschild homology
Prismatic cohomology via topological Hochschild homology
Finally, let us mention how to recover 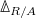 from the topological Homology homology
from the topological Homology homology  . The characteristic 0 story is classical (Quillen, Connes, Tsygan...).
. The characteristic 0 story is classical (Quillen, Connes, Tsygan...).
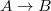 be a map of (commutative) rings. Define the Hochschild homology to be
be a map of (commutative) rings. Define the Hochschild homology to be 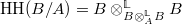 (i.e., derived self-intersection of the diagonal in
(i.e., derived self-intersection of the diagonal in 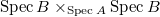 ).
).
We observe:
 .
.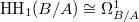
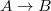 is smooth, then
is smooth, then 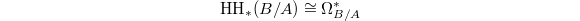 as graded
as graded  -algebras. Moreover, if
-algebras. Moreover, if 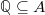 (characteristic 0), then we have a natural decomposition (a lift to the derived category)
(characteristic 0), then we have a natural decomposition (a lift to the derived category) ![$$\mathrm{HH}(B/A)\cong \bigoplus_i \Omega_{B/A}^i[ i].$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_172960909_.gif)
To bring the de Rham differential in, one uses the following observation of Connes:  has an
has an  -action. To see this use
-action. To see this use ![$$\mathrm{HH}(B/A)=B \otimes \mathrm{colim}\big(\xymatrix{\text{two pts }\ar[r] \ar[d] & \text{pt} \\ \text{pt} & }\big)=B \otimes S^1.$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_130660256_.gif) (
( is obtained by gluing two
is obtained by gluing two  's at two points). Then
's at two points). Then ![$[S^1]\in H_1(S^1)$](./latex/BhattEilenberg/latex2png-BhattEilenberg_111089726_-5.gif) induces a map
induces a map  which is the de Rham differential under the previous theorem.
which is the de Rham differential under the previous theorem.
Now let us come to the prismatic story. Let 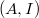 be a perfect prism. Let
be a perfect prism. Let 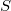 be a smooth algebra over
be a smooth algebra over 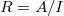 .
.
 , define the topological Hochschild homology
, define the topological Hochschild homology 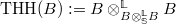 (point: tensoring over the sphere spectrum
(point: tensoring over the sphere spectrum 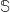 gets rid of the factorials in the denominators). It also has an
gets rid of the factorials in the denominators). It also has an 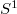 -action, and we similarly define the topological periodic homology
-action, and we similarly define the topological periodic homology 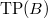 to be the Tate cohomology of
to be the Tate cohomology of 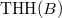 .
.
 be perfectoid. Then
be perfectoid. Then ![$\mathrm{THH}(R)_*=R[u]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_128763766_-5.gif) where
where  has degree 2 (if tensor over
has degree 2 (if tensor over  instead of the sphere spectrum, one gets the divided power algebra), and
instead of the sphere spectrum, one gets the divided power algebra), and ![$\mathrm{TP}_*(R)=A_\mathrm{inf}(R)[u,u^{-1}]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_167258903_-5.gif) .
.
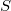 be smooth over a perfectoid
be smooth over a perfectoid  . Then there is a filtration
. Then there is a filtration 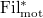 on
on 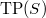 with
with ![$$\mathrm{gr}_\mathrm{mot}^*\mathrm{TP}(S)\cong\Delta_{S/A} \otimes_A A[u,u^{-1}].$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_262129982_.gif)

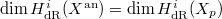 . Then
. Then  has no
has no 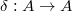 is a map of sets satisfying
is a map of sets satisfying
 ,
, ,
, .
. which is sometime useful.
which is sometime useful.
![$$\xymatrix{W_2(A) \ar[d] \ar[r] &A \ar[d]^{\mathrm{can}}\\ A \ar[r]^{\Fr\circ\mathrm{can}} &A/p.}$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_98665023_.gif)
![$\mathbb{Z}\{x\}=\mathbb{Z}[x_0,x_1,x_2,\ldots]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_164275778_-5.gif) and
and 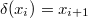 .
.
 such that
such that  . Then
. Then  .
.
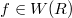 can be written uniquely as a power series
can be written uniquely as a power series ![$$f=\sum_{i\ge0} [a_i] p^i,\quad a_i\in R.$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_203709811_.gif)
 .
.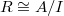 for a perfect prism
for a perfect prism ![$A/I[p^\infty]=A/I[p]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_152671869_-5.gif) . In particular, perfect prisms are bounded.
. In particular, perfect prisms are bounded.
 of
of  .
. , and write
, and write  .
. .
.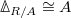 .
.
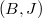 be a
be a 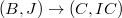 to a prism over
to a prism over 
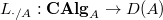 to be
to be 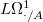 .
.
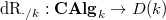 to be
to be 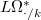 .
.
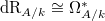 .
.
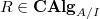 , we have an increasing exhaustive filtration
, we have an increasing exhaustive filtration 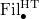 on
on 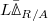 such that
such that ![$$\mathrm{gr}_i^\mathrm{HT}(L\bar\Delta_{R/A})\cong \wedge^iL_{R/(A/I)}[-i]$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_103515244_.gif) in
in  is a commutative algebra object.
is a commutative algebra object. is a commutative algebra object.
is a commutative algebra object.![$R=k[X]=\oplus_{i\in \mathbb{N}}k x^i$](./latex/BhattEilenberg/latex2png-BhattEilenberg_138105512_-5.gif) . Then
. Then ![$R_\mathrm{perf}=k[X^{1/p^\infty}]=\otimes_{i\in \mathbb{N}[1/p]}kx^i$](./latex/BhattEilenberg/latex2png-BhattEilenberg_259216638_-6.gif) .
.
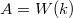 ,
,  identifies with
identifies with 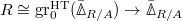 .
.
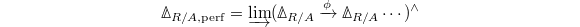 (
( .
.
 (
( (
(![$$R\Gamma_\mathrm{et}(\Spec R[1/p], \mathbb{Z}/p^n)\cong (\Delta_{R/A}[1/d]/p^n)^{\phi=1}.$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_116533049_.gif)
![$\Omega_{R/\mathbb{Z}_p}^* \hat\otimes_{\mathbb{Z}_p} \mathbb{Z}_p[ [q-1]]$](./latex/BhattEilenberg/latex2png-BhattEilenberg_69498991_-9.gif) .
.
 Namely,
Namely,  .
.
 such that
such that ![$\phi(f)\in [p]_q D$](./latex/BhattEilenberg/latex2png-BhattEilenberg_173336650_-5.gif) . Then
. Then ![$$\phi\left(\frac{\phi(f)}{[p]_q}-\delta(f)\right)\in [p]_qD.$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_66816489_.gif)
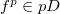 , then
, then 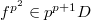 .
.

 where
where  (Theorem
(Theorem  is computed by
is computed by  (by Proposition
(by Proposition 
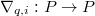 extends uniquely to
extends uniquely to  (a periodic version of
(a periodic version of ![$$\mathrm{HP}(B/A)=\mathrm{H}_\mathrm{Tate}^*(S^1, \mathrm{HH}(B/A)):=\mathrm{Cone}(\mathrm{HH}(B/A)_{hS^1}[ 1 ]\xrightarrow{\mathrm{Nm}} \mathrm{HH}(B/A)^{hS^1}).$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_164640471_.gif)
![$$\mathrm{HP}(B/A)\cong\Omega_{B/A}^* \otimes_A A[u,u^{-1}],$$](./latex/BhattEilenberg/latex2png-BhattEilenberg_214436660_.gif) where
where