This is a note on the construction of Dieudonne modules (over a perfect field), prepared for a student seminar on 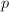 -adic Hodge theory at Harvard, Fall 2012. Our main references are [1] and [2].
-adic Hodge theory at Harvard, Fall 2012. Our main references are [1] and [2].
 Dieudonne modules
Dieudonne modules
Let 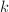 be a perfect field of characteristic
be a perfect field of characteristic  . Our goal is to classify finite (commutative)
. Our goal is to classify finite (commutative) 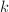 -groups of
-groups of 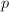 -power order using (semi-)linear algebraic data. Recall every such
-power order using (semi-)linear algebraic data. Recall every such 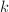 -group can be decomposed as
-group can be decomposed as  Let
Let  be the Frobenius and
be the Frobenius and  be the Verschiebung, then
be the Verschiebung, then
- on
 :
: 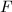 is an isomorphism and
is an isomorphism and  is nilpotent.
is nilpotent. - on
 :
: 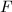 is nilpotent and
is nilpotent and  is nilpotent.
is nilpotent. - on
 :
: 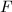 is nilpotent and
is nilpotent and  is an isomorphism.
is an isomorphism.
 is of etale-local type,
is of etale-local type, 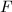 acts as the identity and
acts as the identity and  acts as 0. Dually, the multiplicative group
acts as 0. Dually, the multiplicative group 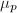 is of local-etale type,
is of local-etale type, 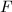 acts as 0 and
acts as 0 and  acts as the identity. The self-dual group
acts as the identity. The self-dual group 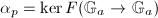 is of local-local type and both
is of local-local type and both 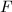 and
and  acts as 0.
acts as 0.
The etale part is relatively easy to deal with: it is same as giving the data of a finite  -module. Over
-module. Over  , the etale part is a constant group of
, the etale part is a constant group of 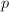 -power order and can be determined by its Pontryagin dual
-power order and can be determined by its Pontryagin dual  . Of course, the local part cannot be detected at the level of points: we would like some enhancement of
. Of course, the local part cannot be detected at the level of points: we would like some enhancement of  to also detect the local part. A natural candidate is using the Witt ring scheme
to also detect the local part. A natural candidate is using the Witt ring scheme  . Let
. Let 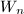 be the ring scheme of Witt vectors of length
be the ring scheme of Witt vectors of length 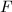 . We have at the level of
. We have at the level of  -points
-points  and in general,
and in general,  Motivated by this, we introduce the local group
Motivated by this, we introduce the local group 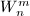 to be the kernel of
to be the kernel of  on
on 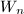 . These are the replacements of
. These are the replacements of  for local groups.
for local groups.
 as
as  Then
Then  and
and  . Moreover, we have exact sequences
. Moreover, we have exact sequences 
 It follows that
It follows that 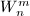 is a successive extension of
is a successive extension of  copies of
copies of  .
.
Staring at the action of  and
and  on
on  motivates the following definition.
motivates the following definition.
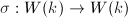 be the automorphism lifting
be the automorphism lifting  on
on 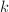 . Let
. Let ![$D_k=W(k)[F,V]$](./latex/latex2png-Dieudonne_149503115_-5.gif) be the Dieudonne ring (noncommutative unless
be the Dieudonne ring (noncommutative unless 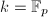 ) subject to the relations
) subject to the relations  ,
, 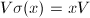 and
and 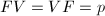 .
.
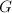 be of local-local type. We define the (contravariant) Dieudonne module of
be of local-local type. We define the (contravariant) Dieudonne module of 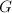 to be
to be 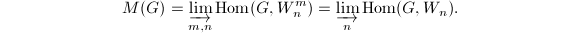 Notice
Notice 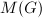 becomes a left
becomes a left 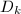 -module via the action of
-module via the action of 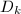 on
on 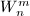 .
.
 on
on 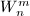 needs to be modified so that it is compatible with the transition maps between the
needs to be modified so that it is compatible with the transition maps between the 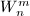 's. Namely, the action of
's. Namely, the action of  on
on 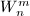 is modified to be multiplication by
is modified to be multiplication by  .
.
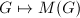 gives an exact anti-equivalence of categories between {finite
gives an exact anti-equivalence of categories between {finite 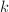 -group schemes of local-local type} and {left
-group schemes of local-local type} and {left 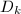 -modules of finite
-modules of finite  -length with
-length with 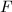 ,
,  nilpotent}.
nilpotent}.
We will not prove this theorem in detail but let us explain why the functor lies in the desired target.
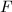 and
and  . The second part follows from induction and the fact that
. The second part follows from induction and the fact that  has
has  -length 1. Notice that
-length 1. Notice that 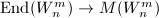 is always injective. To show the surjectivity, one uses the fact that if
is always injective. To show the surjectivity, one uses the fact that if 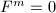 and
and 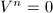 on
on 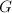 , then any homomorphism
, then any homomorphism 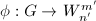 for
for 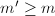 and
and 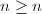 factors uniquely through
factors uniquely through 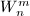 (again by functoriality of
(again by functoriality of 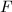 and
and  ).
¡õ
).
¡õ
 . The injectivity is clear since
. The injectivity is clear since  acts non-trivially on
acts non-trivially on 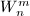 . For the surjectivity, one computes the length of
. For the surjectivity, one computes the length of  as a
as a 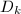 module to be
module to be  , which is equal to
, which is equal to  .
.
For a general finite 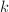 -group, we define its Dieudonne module for the three parts in its decomposition separately.
-group, we define its Dieudonne module for the three parts in its decomposition separately.
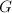 is etale-local, then we define
is etale-local, then we define 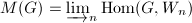 . Suppose
. Suppose 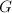 is local-etale, then we define
is local-etale, then we define  , where the dual outside is given by
, where the dual outside is given by ![$M^\vee=\Hom_{W(k)}(M, W(k)[1/p]/W(k))$](./latex/latex2png-Dieudonne_224878624_-6.gif) . In general, we decompose
. In general, we decompose 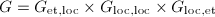 and define its (contravariant) Dieudonne module
and define its (contravariant) Dieudonne module 
 . This reduces to the local-local case, which essentially reduces to the duality between
. This reduces to the local-local case, which essentially reduces to the duality between 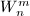 and
and  .
.
Let us also mention an important property that recovers the cotangent space of 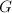 from its Dieudonne module.
from its Dieudonne module.
![$$T_{G,0}:=\ker (G(k[\varepsilon])\rightarrow G(k))\cong \Hom(G^\vee, \mathbb{G}_a)=\Hom(G^\vee,W_1).$$](./latex/latex2png-Dieudonne_21493773_.gif) Since
Since 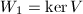 on any
on any  , we know that
, we know that 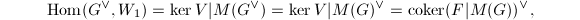 as desired.
¡õ
as desired.
¡õ
 :
:  Oda [3] proved that
Oda [3] proved that  is canonically isomorphic to
is canonically isomorphic to ![$M=M(A[p])$](./latex/latex2png-Dieudonne_9212889_-5.gif) over any perfect field of characteristic
over any perfect field of characteristic  and the Hodge filtration
and the Hodge filtration  can be identified with
can be identified with  .
.
We summarize the main theorem of Dieudonne theory as follows.
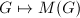 between {finite
between {finite 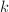 -group schemes of
-group schemes of 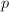 -power order} and {left
-power order} and {left 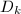 -modules of finite
-modules of finite  -length}.
satisfying:
-length}.
satisfying:
 .
. .
. is canonically isomorphic to the cotangent space of
is canonically isomorphic to the cotangent space of 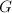 .
.- (extension of scalars) for any extension
 of perfect fields,
of perfect fields,  .
.
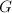 is of order
is of order 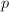 . Then
. Then 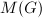 is a
is a  -module of rank 1 and
-module of rank 1 and  acts as 0 on
acts as 0 on 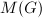 . Hence
. Hence  is a one dimensional
is a one dimensional 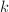 -vector space with the action of
-vector space with the action of 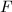 and
and  .
.
- For
 ,
, 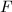 acts as
acts as  and
and  acts as 0.
acts as 0. - For
 ,
, 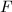 acts as 0 and
acts as 0 and  acts as
acts as  .
. - For
 , both
, both 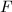 and
and 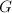 acts as 0.
acts as 0.
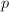 -divisible groups over
-divisible groups over 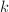 (of height
(of height  ) and left
) and left 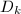 -modules which are free as
-modules which are free as  -modules (of rank
-modules (of rank  ).
).
 Fontaine's uniform construction
Fontaine's uniform construction
One unsatisfying aspect of the above construction of the Dieudonne functor is that definition for the local-etale (multiplicative) part seems a bit artificial. In the second part of this talk, we shall describe a uniform construction due to Fontaine.
 is a
is a 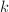 -algebra. By shifting to the left, we see that every element of
-algebra. By shifting to the left, we see that every element of  is represented by a covector
is represented by a covector 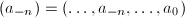 ,
,  . Let
. Let 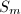 be the
be the 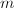 -th universal addition polynomial for Witt vectors, then the addition rule on covectors
-th universal addition polynomial for Witt vectors, then the addition rule on covectors  is given by
is given by  for
for 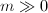 (which stabilizes). We denote the
(which stabilizes). We denote the 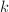 -group scheme obtained this way by
-group scheme obtained this way by  , called the group of unipotent Witt covectors. This is simply a reformulation of what we used to detect the unipotent part of finite
, called the group of unipotent Witt covectors. This is simply a reformulation of what we used to detect the unipotent part of finite 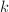 -group schemes of power order.
-group schemes of power order.
In order to also detect the multiplicative part, Fontaine generalizes it to the following.
 is a
is a 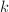 -algebra. We define
-algebra. We define  to consist of
to consist of  ,
,  for which there exists
for which there exists 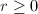 such that the ideal generated by
such that the ideal generated by 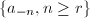 is nilpotent. Then
is nilpotent. Then  and indeed the addition rule also extends to
and indeed the addition rule also extends to  . We call the
. We call the 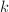 -group scheme
-group scheme  the group of Witt covectors. In particular,
the group of Witt covectors. In particular,  .
.
 with the discrete topology and
with the discrete topology and  with the induced subspace topology from the product topology. Then
with the induced subspace topology from the product topology. Then  becomes a complete and separated topological group. Endow
becomes a complete and separated topological group. Endow 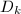 with the
with the 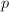 -adic topology from
-adic topology from  , then
, then  acts on
acts on  continuously and makes
continuously and makes  a topological
a topological 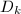 -module, which is torsion, complete and separated.
-module, which is torsion, complete and separated.
Now we can define the Dieudonne module for the larger category of formal 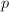 -groups over
-groups over 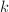 using
using 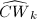 .
.
 is the affine algebra of
is the affine algebra of 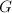 , then
, then  is closed under the topology defined above. So
is closed under the topology defined above. So  is also a topological
is also a topological 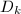 -module. Moreover, one can check it is
-module. Moreover, one can check it is ![$W(k)[F]$](./latex/latex2png-Dieudonne_264375767_-5.gif) -profinite, i.e., as a
-profinite, i.e., as a ![$W(k)[F]$](./latex/latex2png-Dieudonne_264375767_-5.gif) -module, the quotient by any of its open submodules has finite length.
-module, the quotient by any of its open submodules has finite length.
![$W(k)[F]$](./latex/latex2png-Dieudonne_264375767_-5.gif) -profinite topological
-profinite topological 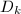 -module
-module 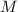 , we define
, we define 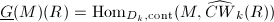 for any finite
for any finite 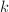 -algebra
-algebra  . Then
. Then 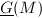 is a formal
is a formal 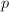 -group over
-group over 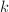 (as it is left exact).
(as it is left exact).
 gives an exact anti-equivalence of categories between {formal
gives an exact anti-equivalence of categories between {formal 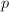 -group schemes over
-group schemes over 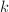 } and {
} and {![$W(k)[F]$](./latex/latex2png-Dieudonne_264375767_-5.gif) -profinite topological
-profinite topological 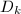 -modules}.
-modules}. 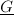 is its quasi-inverse.
is its quasi-inverse.
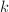 -groups of
-groups of 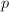 -power order and the subcategory of
-power order and the subcategory of 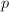 -divisible groups over
-divisible groups over 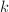 , we recover the classical Dieudonne functor with all the desired properties.
, we recover the classical Dieudonne functor with all the desired properties.
References
[1]Finite group schemes, 2004, www.math.ethz.ch/~pink/ftp/FGS/CompleteNotes.pdf .
[2]Groupes p-divisibles sur les corps locaux, Société mathématique de France, 1977.
[3]The first de Rham cohomology group and Dieudonné modules, Ann. Sci. Ecole Norm. Sup.(4) 2 (1969), no.1, 63--135.
 annihilate
annihilate  .
.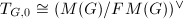 .
.
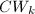 from finite
from finite 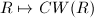 is pro-represented by a formal
is pro-represented by a formal  , where
, where ![$$k^0[{}[X]]=\varprojlim_{r,s} k[\ldots,X_{-n},\ldots,X_0]/\mathfrak{a}_r^s, \quad \mathfrak{a}_r=(X_{-n},n\ge r).$$](./latex/latex2png-Dieudonne_50952496_.gif)
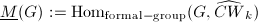 .
.