These are my live-TeXed notes (reorganized according to my tastes) for the course Discrete subgroups of Lie groups and discrete transformation groups by Professor Lizhen Ji, July 19 — August 9, at Math Science Center of Tsinghua University.
 The plan of this course
The plan of this course
- Introduction and basic notions
- General questions on discrete subgroups and discrete transformation groups.
- Fuchsian groups, namely discrete subgroups of
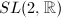 (
( ). In particular, the modular group
). In particular, the modular group 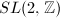 and its congruence subgroups. Kleinian groups, namely discrete subgroups of
and its congruence subgroups. Kleinian groups, namely discrete subgroups of  . They provide special, important examples of lattices of semisimple Lie groups and also nonlattices.
. They provide special, important examples of lattices of semisimple Lie groups and also nonlattices. - Crystallographic groups (Bieberbach theorems)
- Nilpotent Lie groups and their lattices
- Solvable Lie groups and their lattices (Mostow rigidity)
- Semisimple Lie groups and their lattices
The main purpose of this course is to study lattices of semisimple Lie groups. But we need to understand lattices of non-semisimple Lie groups too. (Unfortunately, only the first three topics were covered in this course).
 Introduction
Introduction
The topic of this course is a central subject of modern mathematics. It is closely related to many areas, e.g., group theory, geometry (differential geometry, algebraic geometry, arithmetic geometry), analysis, number theory (automorphic forms) and algebra (algebraic  -theory).
-theory).
Major figures in this subject includes Poincare, Klein, Fricke, and recently C. L. Siegel, A. Weil, A. Selberg, A. Borel, Harish-Chandra, Piatetski-Shapiro, G. Margulis, D. Kazhdan, Maltsev, Auslander, Hsien-Chung Wang, R. Langlands. Two important books are Raghunathan's and Zimmer's.
Now let us explain the "what, why and how" of the words in the course title.
This definition is not very interesting at first sight since the discrete topology may not appear "naturally".
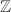 with the natural topology.
with the natural topology.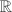 with the discrete topology. But the usual topology is more natural since it is a connected Lie group. The inclusion of
with the discrete topology. But the usual topology is more natural since it is a connected Lie group. The inclusion of 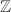 into
into 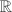 induces the usual discrete topology on
induces the usual discrete topology on 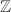 .
.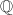 with the discrete topology. The induced topology of
with the discrete topology. The induced topology of 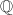 from
from 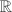 is not discrete. Nevertheless, The discrete topology on
is not discrete. Nevertheless, The discrete topology on 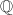 is natural and important since it can be realized as a discrete subgroup of an important locally compact topological space, i.e., the ring of adeles.
is natural and important since it can be realized as a discrete subgroup of an important locally compact topological space, i.e., the ring of adeles.
 be a topological group (usually we assume
be a topological group (usually we assume  is locally compact). A subgroup
is locally compact). A subgroup 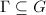 is called a discrete subgroup if the induced topological on
is called a discrete subgroup if the induced topological on  is discrete.
is discrete.
Here is a less trivial example.
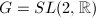 . Then
. Then 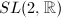 is a Lie group since it is the inverse image of the regular value 1 under
is a Lie group since it is the inverse image of the regular value 1 under 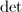 (or, it is a closed subgroup of a Lie group). The modular group
(or, it is a closed subgroup of a Lie group). The modular group 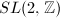 is a discrete subgroup of
is a discrete subgroup of 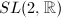 since
since  is discrete in
is discrete in  . Also,
. Also, 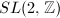 is a discrete subgroup of
is a discrete subgroup of 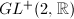 and
and 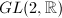 . The first one of the three embeddings is the most natural one. Firstly,
. The first one of the three embeddings is the most natural one. Firstly, 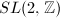 is a lattice, namely
is a lattice, namely 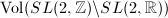 is finite, but
is finite, but 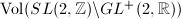 is infinite. Secondly, from the point of view of algebraic groups,
is infinite. Secondly, from the point of view of algebraic groups, 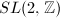 is an arithmetic subgroup of the semisimple linear algebraic group
is an arithmetic subgroup of the semisimple linear algebraic group 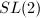 and
and 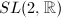 is the
is the 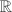 -locus of
-locus of 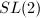 .
.
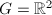 , for any nonzero vector
, for any nonzero vector 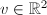 , we have an embedding
, we have an embedding 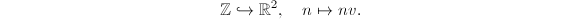 Also, given two linear independent vectors
Also, given two linear independent vectors 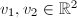 , we have an embedding
, we have an embedding 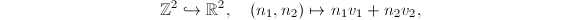 which is more natural since
which is more natural since 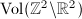 is finite. In other words, we are interested in discrete subgroups
is finite. In other words, we are interested in discrete subgroups  of
of  that are not "too small" in
that are not "too small" in  .
.
Now let us come to the second key word in the course title — transformation groups, which first appeared in Lie's book Theorie der transformations gruppe I, II, II.
 be a topological group and
be a topological group and  be a topological space. A topological action of
be a topological space. A topological action of  on
on  is a continuous map
is a continuous map 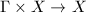 satisfying
satisfying
 for any
for any 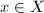 ,
,- for any
 and any
and any 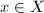 ,
,  .
.
For any 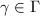 , the
, the  -action is a homeomorphism. Let
-action is a homeomorphism. Let  be the group of homeomorphisms of
be the group of homeomorphisms of  , then we get a homomorphism
, then we get a homomorphism  . The following two concepts are closely related.
. The following two concepts are closely related.
We can even put more structures on the spaces  and the groups
and the groups  :
:
 is a manifold,
is a manifold,  is either a discrete group or a Lie group and the action is by diffeomorphisms. This is the subject of the classical transformation group theory.
is either a discrete group or a Lie group and the action is by diffeomorphisms. This is the subject of the classical transformation group theory. is a complex manifold (or complex space),
is a complex manifold (or complex space),  is either discrete or a complex Lie group and the action is by holomorphisms.
is either discrete or a complex Lie group and the action is by holomorphisms. is an algebraic variety,
is an algebraic variety,  is an algebraic group and the action is by morphisms.
is an algebraic group and the action is by morphisms.
We are interested in the case that  is an infinite discrete group and
is an infinite discrete group and  is a topological space or manifold, which is important for, e.g., geometric group theory.
is a topological space or manifold, which is important for, e.g., geometric group theory.
 be a Hausdorff space with
be a Hausdorff space with  -action on
-action on  . We say the action of
. We say the action of  is discontinuous, if for any
is discontinuous, if for any 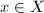 , the orbit
, the orbit 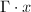 of
of  is a discrete subset of
is a discrete subset of  . We say the action of
. We say the action of  is properly discontinuous, if for any compact subset
is properly discontinuous, if for any compact subset 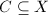 , the set
, the set 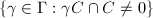 is finite.
is finite.
 -action on
-action on  is properly discontinuous, then the quotient
is properly discontinuous, then the quotient 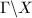 with the quotient topology is Hausdorff.
with the quotient topology is Hausdorff.
Here are a few reasons why we study discrete subgroups.
- It occurs naturally (e.g.,
 ).
). - It provides important examples in geometric group theory and combinatorial group theory.
- Given a manifold
 with nontrivial fundamental group, then
with nontrivial fundamental group, then  acts on
acts on  as Deck transformations.
as Deck transformations. - Many natural spaces arises from quotients
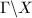 (e.g., locally symmetric space).
(e.g., locally symmetric space).
Groups are interesting in themselves, to understand their properties, the "only" effective way is to use their actions on suitable spaces. So groups that admit good actions on nice spaces are interesting and special. Besides discrete subgroups of Lie groups, two other very important discrete transformation groups are:
- Mapping class groups of surfaces with the actions on the Teichmuller spaces.
- Let
 be the free group on
be the free group on  generators, the outer automorphism group
generators, the outer automorphism group  is the most important group in combinatorial group theory. In 1980, Culler-Vogtmann discovered the Outer space
is the most important group in combinatorial group theory. In 1980, Culler-Vogtmann discovered the Outer space  , a contractible space (which is a simplicial complex) where
, a contractible space (which is a simplicial complex) where  acts simplically and properly.
acts simplically and properly.  is the space of marked metrics, which is related to the hot topic of tropical geometry.
is the space of marked metrics, which is related to the hot topic of tropical geometry.
 of a topological group
of a topological group  is called a uniform lattice if
is called a uniform lattice if 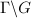 is compact.
is compact.
- Every discrete subgroup
 of
of  is of the form
is of the form  where
where  's are linearly independent.
's are linearly independent.  is a uniform lattice if and only if
is a uniform lattice if and only if  is finite.
is finite.
We can define the more general notion of volume on the quotient 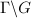 using a fundamental set of the
using a fundamental set of the  -action on
-action on  .
.
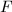 of
of  is called a fundamental set for the
is called a fundamental set for the  -action on
-action on  if
if 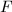 meets every
meets every 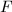 -orbit exactly once, namely
-orbit exactly once, namely 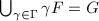 and
and 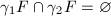 for any
for any 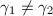 in
in  .
.
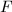 by the axiom of choice, i.e., by picking one element from each orbit. However, it may not be a Borel subset.
by the axiom of choice, i.e., by picking one element from each orbit. However, it may not be a Borel subset.
 be a secondly countable locally compact topological group and
be a secondly countable locally compact topological group and  be a left invariant Haar measure on
be a left invariant Haar measure on  , then for any discrete subgroup
, then for any discrete subgroup  of
of  , there exists an induced measure on
, there exists an induced measure on 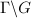 .
.
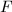 . Since
. Since  is a discrete subgroup of
is a discrete subgroup of  , there exists an open subset
, there exists an open subset  containing the identity such that
containing the identity such that  . Since
. Since  is a topological group , there exists an open neighbourhood
is a topological group , there exists an open neighbourhood 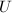 containing
containing  such that
such that  . Then the
. Then the  -translates of
-translates of 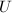 are disjoint. Since
are disjoint. Since  is secondly countable, there exists a sequence
is secondly countable, there exists a sequence  of
of  such that
such that  . Now let
. Now let  one can check that
one can check that 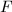 is a Borel fundamental set.
is a Borel fundamental set.
Let  be the projection. Then
be the projection. Then  is one-to-one. Define an induced measure
is one-to-one. Define an induced measure  on
on 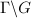 by
by  where
where  is a Borel subset of
is a Borel subset of 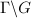 . We need to show that this induced meausre is independent on the choice of
. We need to show that this induced meausre is independent on the choice of 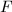 . Suppose
. Suppose  are two Borel fundamental sets. Then it suffices to show that
are two Borel fundamental sets. Then it suffices to show that  for any subset
for any subset  which is invariant under
which is invariant under  . By the invariance of
. By the invariance of  and the definition of
and the definition of  , we have
, we have This completes the proof.
¡õ
This completes the proof.
¡õ
 of a locally compact topological group
of a locally compact topological group  is called a lattice (or lattice subgroup) if
is called a lattice (or lattice subgroup) if 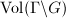 is finite. In other words, let
is finite. In other words, let 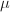 be a left invariant measure on
be a left invariant measure on  , a discrete subgroup
, a discrete subgroup  is called a lattice if
is called a lattice if 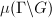 is finite, where
is finite, where 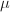 is the induced meausre on
is the induced meausre on 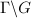 .
.
Let  be a locally compact topological group. Then
be a locally compact topological group. Then  admits a left invariant Haar measure unique up to multiple. Let
admits a left invariant Haar measure unique up to multiple. Let  be a left invariant Haar measure and let
be a left invariant Haar measure and let  be the right action, then
be the right action, then  induces a measure
induces a measure  and
and  is also left invariant. By the uniqueness of left invariant Haar measure, there exists a constant
is also left invariant. By the uniqueness of left invariant Haar measure, there exists a constant 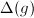 such that
such that  .
.
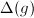 is called the modular function of
is called the modular function of  . If
. If 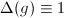 , the
, the  is called unimodular (hence any left invariant Haar measure is also right invariant).
is called unimodular (hence any left invariant Haar measure is also right invariant).
 be a real semisimple Lie group, then
be a real semisimple Lie group, then  is unimodular, since the modular function
is unimodular, since the modular function 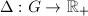 is homomorphism,
is homomorphism, 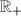 is abelian and
is abelian and ![$G=[G,G]$](./latex/latex2png-DiscreteSubgroups_13762369_-5.gif) .
.
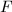 such that
such that 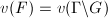 . One can check that for any
. One can check that for any 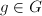 ,
, 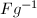 is also a fundamental set. So
is also a fundamental set. So 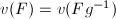 (finite) and
(finite) and  is unimodular.
¡õ
is unimodular.
¡õ
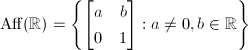 is not unimodular, as the measure
is not unimodular, as the measure 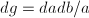 is left invariant but not right invariant. Hence it doesn't admit lattices. Similarly the
is left invariant but not right invariant. Hence it doesn't admit lattices. Similarly the 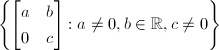 is not unimodular, hence it doesn't admit lattices either.
is not unimodular, hence it doesn't admit lattices either.
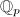 is abelian but doesn't have any notrivial discrete subgroups. If
is abelian but doesn't have any notrivial discrete subgroups. If 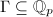 is a discrete subgroup containing
is a discrete subgroup containing 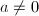 , then
, then 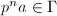 but
but 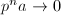 , contradicting the fact that
, contradicting the fact that  is discrete.
is discrete.
It is still an open problem to decide when a unimodular Lie group group admits lattices. Nevertheless, the anwser is affirmative for semisimple Lie groups.
 is a real semisimple Lie group with finitely many connected components, then
is a real semisimple Lie group with finitely many connected components, then  admits lattices (both uniform and nonuniform).
admits lattices (both uniform and nonuniform).
 Questions and problems about discrete subgroups
Questions and problems about discrete subgroups
We start by listing several problems concerning a discrete subgroup  to motivate our discussion.
to motivate our discussion.
Finite generation Namely, find finitely many elements  such that every element of
such that every element of  can be written as
can be written as  where
where  . The existence of the generation is relatively easy (e.g., Kazhdan property (T)). However, finding the explicit generators are generally much harder, e.g., how about the generators of
. The existence of the generation is relatively easy (e.g., Kazhdan property (T)). However, finding the explicit generators are generally much harder, e.g., how about the generators of 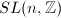 for
for 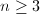 ? The finite generation is useful for geometric group theory (word metric, Cayely graph, etc.)
? The finite generation is useful for geometric group theory (word metric, Cayely graph, etc.)
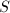 be a set of generators of
be a set of generators of  . Define
. Define 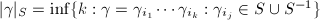 . Define the word metric
. Define the word metric 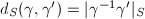 for any
for any 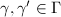 . This metric is left invariant under
. This metric is left invariant under  , namely
, namely 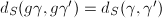 .
.
 consists of the elements of
consists of the elements of  as vertices. An edge between
as vertices. An edge between  exists if and only if
exists if and only if  . Then
. Then 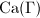 is connected.
is connected.
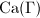 is a metric space by declaring that every edge has length 1. Then the metric space
is a metric space by declaring that every edge has length 1. Then the metric space 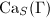 is quasi-isometric to
is quasi-isometric to  .
. 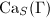 is connected but is not simply connected in general.
is connected but is not simply connected in general.
Finite presentation Let  be a finitely generated group, we may ask whether there are only finitely many relations between the generators. Finding the existence and explicit relations are very important (and hard) in combinatorial group theory.
be a finitely generated group, we may ask whether there are only finitely many relations between the generators. Finding the existence and explicit relations are very important (and hard) in combinatorial group theory.
Cohomology  and
and  can be defined as the cohomology groups and homology groups of the classifying space
can be defined as the cohomology groups and homology groups of the classifying space  . These are important invariants of
. These are important invariants of  useful in topology, number theory, representation theory and differential geometry.
useful in topology, number theory, representation theory and differential geometry.
We are interested in knowing the conditions under which good models (closed manifolds) exist for the classifying space  . Furthermore, if
. Furthermore, if  can be realized by a closed manifold, the Borel conjecture asks whether it is unique up to homeomorphism.
can be realized by a closed manifold, the Borel conjecture asks whether it is unique up to homeomorphism.
Large scale geometry The geometric group theory single-handedly established by Gromov asks how "big"  is, roughly speaking, the growth rate of the volumes of the balls in
is, roughly speaking, the growth rate of the volumes of the balls in  . For example,
. For example,  is "smaller" than the Poincare upper half plane
is "smaller" than the Poincare upper half plane  : the volume
: the volume  in
in  , but
, but  in
in  grows exponentially.
grows exponentially.
For  , we consider the asymptotic behaviors of the volume
, we consider the asymptotic behaviors of the volume  .
.
The following striking result due to Gromov relates the large scale geometry of a group to its own algebraic structure.
 is a lattice of a nilpotent Lie group, then
is a lattice of a nilpotent Lie group, then  has a polynomial growth. Conversely, if
has a polynomial growth. Conversely, if  has a polynomial growth, then
has a polynomial growth, then  is virtually nilpotent, namely there exists a finite index subgroup
is virtually nilpotent, namely there exists a finite index subgroup 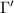 of
of  such that
such that 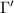 is a lattice in a nilpotent Lie group.
is a lattice in a nilpotent Lie group.
Rigidity and action on manifolds Mostow strong rigidity, Margulis super-rigidity, Zimmer program, etc..
Construction and classification of infinite simple groups Margulis normal subgroup theorem and the rough classification up to quasi-isometry.
 is an irreducible lattice in a semisimple Lie group of rank
is an irreducible lattice in a semisimple Lie group of rank 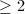 . Then every normal subgroup of
. Then every normal subgroup of  is finite or of finite index.
is finite or of finite index.
Now let us list some problems concerning a discrete transformation group  acting on
acting on  .
.
Properness If  acts on
acts on  properly, the the quotient space
properly, the the quotient space 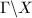 is a Hausdorff sapce. Nevertheless, We are also interested in non-proper actions such as ergodic actions (chaotic actions). They are important in Mostow rigidity, Margulis' work and also number theory.
is a Hausdorff sapce. Nevertheless, We are also interested in non-proper actions such as ergodic actions (chaotic actions). They are important in Mostow rigidity, Margulis' work and also number theory.
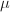 be a measure on
be a measure on  invariant under
invariant under  , the action of
, the action of  is called ergodic if any invariant subset of
is called ergodic if any invariant subset of  is either of measure 0 or of full measure.
is either of measure 0 or of full measure.
Orbits and quotient space Suppose  acts properly on
acts properly on  , we would like to understand structures (geometry, topology, analsis) of orbits of
, we would like to understand structures (geometry, topology, analsis) of orbits of  in
in  and the quotient
and the quotient 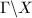 .
.
- Geometry: the geometry of locally symmetic spaces
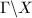 when
when  is a symmetic space;
is a symmetic space; - Topology: often
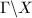 provides classification spaces like the classifying spaces.
provides classification spaces like the classifying spaces. - Analysis: spectual theorem of automorphic forms. The Selberg trace formular relates the geometry and analysis.
A crucial role is played by finding good fundamental domains of  .
.
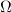 in
in  (somewhere between closed and open) is called a fundamental domain for
(somewhere between closed and open) is called a fundamental domain for  in
in  if
if  and the interiors of
and the interiors of  's are disjoint (cf. Definition 8).
's are disjoint (cf. Definition 8).
Usually we require that 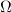 is not too complicated, e.g., the boundary of
is not too complicated, e.g., the boundary of 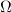 is small:
is small:  . If
. If  has a measure
has a measure  invariant under
invariant under  , we usually require that
, we usually require that  . If
. If  is a manifold, we usually require that
is a manifold, we usually require that  consists of submanifolds of smaller dimensions.
consists of submanifolds of smaller dimensions.
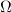 is called locally finite if for any
is called locally finite if for any 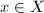 , there exists a neighbourhood
, there exists a neighbourhood 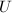 containing
containing  such that
such that 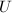 only meets finitely many
only meets finitely many  -translates of
-translates of 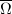 . A fundamental domain
. A fundamental domain 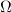 is called globally finite if
is called globally finite if 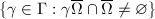 is fintie.
is fintie.
Suppose 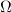 is a fundamental domain. Let
is a fundamental domain. Let  be the projection. Then
be the projection. Then  is obtained by identifying some points on the boundary
is obtained by identifying some points on the boundary  , namely we have a continuous bijection
, namely we have a continuous bijection  . The significance of the local finiteness and global finiteness can be seen from the following two theorems.
. The significance of the local finiteness and global finiteness can be seen from the following two theorems.
 is a connected topological space and
is a connected topological space and  acts properly on
acts properly on  . Let
. Let 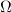 be a fundamental domain. Assume
be a fundamental domain. Assume 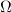 is open and
is open and 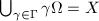 . Let
. Let 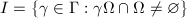 . If
. If 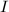 is finite, then
is finite, then  is finitely generated. Briefly speaking, if
is finitely generated. Briefly speaking, if  admits a globally finite fundamental domain then
admits a globally finite fundamental domain then  is finitely generated.
is finitely generated.
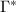 be the subgroup generated by
be the subgroup generated by 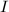 . We claim that
. We claim that 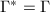 . If not, then by the construction of
. If not, then by the construction of  ,
, 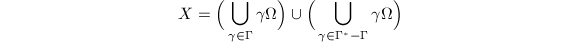 decomposes as two disjoint open subsets, which contradicts the assumption that
decomposes as two disjoint open subsets, which contradicts the assumption that  is connected.
¡õ
is connected.
¡õ
Finding fundamental domains with global finiteness for lattices in Lie groups is called reduction theory. Legendre and Gauss started this theory while studying number-theoretic problems. The finiteness property is now called Siegel finiteness.
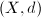 be a proper (i.e., every bounded closed subset is compact) metric space. Let
be a proper (i.e., every bounded closed subset is compact) metric space. Let  acts isometrically. We define the Dirichlet fundamental domain
acts isometrically. We define the Dirichlet fundamental domain 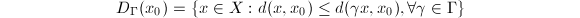 for
for 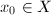 not fixed by any nontrivial element of
not fixed by any nontrivial element of  . In other words, we pick the elements which are closest to
. In other words, we pick the elements which are closest to 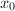 in each
in each  -orbit to form
-orbit to form 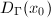 . It is clear that
. It is clear that 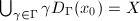 , however, the boundary may be huge. Nevertheless, we know that
, however, the boundary may be huge. Nevertheless, we know that 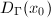 is a fundamental domain in the following special case.
is a fundamental domain in the following special case.
 be a Riemannian manifold and
be a Riemannian manifold and 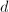 be the Riemannian distance. Then
be the Riemannian distance. Then 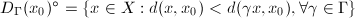 and
and 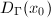 is a fundamental domain.
is a fundamental domain.
We can also relax the requirement on the domain in the proof of Theorem 5.
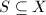 is called a rough (coarse) fundamental domain for
is called a rough (coarse) fundamental domain for  , if
, if 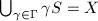 and the induces map
and the induces map 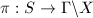 is finite-to-one, i.e., the size of the fibres are bounded.
is finite-to-one, i.e., the size of the fibres are bounded.
 be a connected topological space. If
be a connected topological space. If 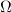 is a rough fundamental domain (open or closed) and
is a rough fundamental domain (open or closed) and 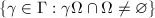 if finite, then
if finite, then  is finitely generated.
is finitely generated.
 Fuchsian groups
Fuchsian groups
We shall study the Fuchsian groups in the general framework of discrete subgroups of semisimple Lie groups.
Recall that 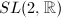 acts on
acts on 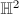 holomorphically and isometrically by Mobius transformations. This action is transitive, i.e., for any
holomorphically and isometrically by Mobius transformations. This action is transitive, i.e., for any  , there exists
, there exists  such that
such that  . The stablizer of
. The stablizer of  is
is  , hence
, hence  . If
. If  is a discrete subgroup of
is a discrete subgroup of 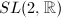 , then
, then  acts properly on
acts properly on 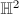 .
.
Fuchsian groups divide into two types:
- the first kind: if the limit set of
 in the boundary
in the boundary  is the whole boundary.
is the whole boundary. - the seconnd kind: if it is not of the first kind.
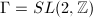 be the modular group, then
be the modular group, then  is a lattice, therefore it is a Fuchsian group of the first kind. Note that
is a lattice, therefore it is a Fuchsian group of the first kind. Note that 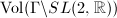 is finite if and only if
is finite if and only if 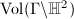 is finite. The latter also follows from the well-known explicit description of the fundamental domain of
is finite. The latter also follows from the well-known explicit description of the fundamental domain of 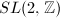 :
: 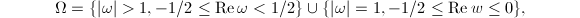 which is also a Dirichlet fundamental domain
which is also a Dirichlet fundamental domain 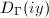 for
for  . In this case, the strip
. In this case, the strip 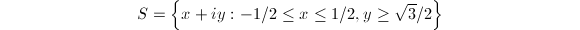 is a rough fundamental domain. Since the integration of
is a rough fundamental domain. Since the integration of 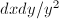 is bounded on
is bounded on 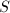 , we know that
, we know that  is a lattice. Also, Proposition 7 implies that
is a lattice. Also, Proposition 7 implies that 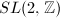 is not a uniform.
is not a uniform.
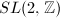 appeared early in Gauss' Disquisitiones Arithmeticae when he studied the problem of representing integers by quadratic forms. The space of all positive definite quadratic forms corresponds to the space of all positive definite
appeared early in Gauss' Disquisitiones Arithmeticae when he studied the problem of representing integers by quadratic forms. The space of all positive definite quadratic forms corresponds to the space of all positive definite  matrices. Note that
matrices. Note that 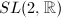 acts on all positive definite matrices of determinant 1 by
acts on all positive definite matrices of determinant 1 by  transitively and the stabilizer of
transitively and the stabilizer of 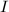 is
is  , so the space of all positive definite
, so the space of all positive definite  matrices of determinant 1 corresponds to
matrices of determinant 1 corresponds to  . For
. For  , the quadratic forms
, the quadratic forms  and
and  take the same set of values on integers
take the same set of values on integers  . So this problem boils down to finding the simplest quadratic form in each
. So this problem boils down to finding the simplest quadratic form in each 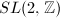 orbit. The reduction process goes by starting with any quadratic form and reducing it to the simplest one.
orbit. The reduction process goes by starting with any quadratic form and reducing it to the simplest one.
An important part of Minkowskii's geometry of numbers consists of reduction theory of finding fundamental domains of 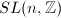 on
on  or
or  on
on  .
.
 is a complete Riemannian manifold,
is a complete Riemannian manifold,  acts properly and isometrically on
acts properly and isometrically on  , then the Dirichlet fundamental domain
, then the Dirichlet fundamental domain 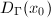 is locally finite.
is locally finite.
If  is torsion-free, then
is torsion-free, then  acts freely on
acts freely on 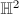 and
and  is a covering map. However,
is a covering map. However, 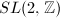 is not torsion-free and some elements of
is not torsion-free and some elements of 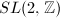 fix points in
fix points in 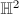 . Nevertheless,
. Nevertheless, 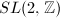 admits finite index torsion-free subgroups. For such a torsion-free subgroup
admits finite index torsion-free subgroups. For such a torsion-free subgroup 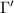 ,
,  is a covering map from a smooth manifold to a orbifold. Minkowskii showed that when
is a covering map from a smooth manifold to a orbifold. Minkowskii showed that when  , the principal congruence subgroup
, the principal congruence subgroup  is torsion-free.
is torsion-free.
The following more general result is due to Selberg.
 is a finitely generated subgroup of
is a finitely generated subgroup of 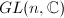 , then
, then  admits a finite index torsion-free subgroup.
admits a finite index torsion-free subgroup.
In particular, every finitely generated Fuchsian group admits a finite index torsion-free subgroup.
 is called linear if it can be embedded into some
is called linear if it can be embedded into some 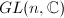 . So a finitely generated subgroup
. So a finitely generated subgroup  of a linear Lie group
of a linear Lie group  admits a finite index torsion-free subgroup
admits a finite index torsion-free subgroup 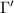 . However, if
. However, if  is not linear, this is not necessarily true.
is not linear, this is not necessarily true.
 of a Lie group
of a Lie group  finitely generated?
finitely generated?
More generally, we have:
We shall discuss the idea of the proof of Theorem 6.
Let 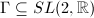 be a Fuchsian group, then the Dirichlet fundamental domains
be a Fuchsian group, then the Dirichlet fundamental domains 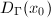 are bounded by geodesics because the bisector
are bounded by geodesics because the bisector  is a geodesic.
is a geodesic.
 is called geometrically finite if it admits a fundamental domain that is bounded by finitely many geodesics (called a geodesic polygon).
is called geometrically finite if it admits a fundamental domain that is bounded by finitely many geodesics (called a geodesic polygon).
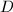 is a fundamental domain of
is a fundamental domain of  bounded by finitely many geodesics in
bounded by finitely many geodesics in 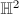 , then there exists a pairing of sides of
, then there exists a pairing of sides of 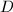 by elements of
by elements of  . In other words, for any geodesic side
. In other words, for any geodesic side 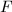 , there exists another side
, there exists another side 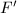 and an element
and an element 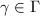 such that
such that 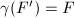 . In fact, by definition, the
. In fact, by definition, the  -translates of
-translates of 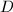 cover
cover 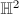 without overlap in the interior. So there exists a translate
without overlap in the interior. So there exists a translate 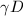 such that
such that 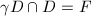 , which implies that there exists
, which implies that there exists 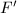 such that
such that 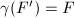 . Note that
. Note that 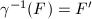 , so this gives a pairing of all sides of
, so this gives a pairing of all sides of 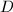 .
.
Let  be elements of
be elements of  that pairs the sides of
that pairs the sides of 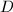 . We claim that these elements
. We claim that these elements  generates the whole group
generates the whole group  . In fact, we can reach the translate
. In fact, we can reach the translate 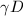 by a chain of neighbouring translates of
by a chain of neighbouring translates of 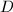 , which lies in
, which lies in  .
¡õ
.
¡õ
The Siegel Theorem 6then follows from Proposition 10and the following theorem.
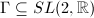 is a lattice, then every Dirichlet fundamental domain of
is a lattice, then every Dirichlet fundamental domain of  in
in 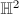 has only finitely many geodesic sides, hence
has only finitely many geodesic sides, hence  is geometrically finite.
is geometrically finite.
We have proved that a geometrically finite Fuchsian group is finitely generates. The following converse is also true for Fuchsian groups.
The hyperbolic plane 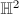 is a two dimensional simply connected complete Riemannian manifold of constant curvature -1. For each dimension, we have a unique hyperbolic space
is a two dimensional simply connected complete Riemannian manifold of constant curvature -1. For each dimension, we have a unique hyperbolic space  with this property, which is given by
with this property, which is given by  with metric
with metric 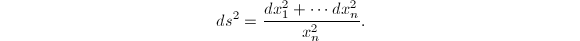
 is a discrete group acting isometrically and properly discontinuously on
is a discrete group acting isometrically and properly discontinuously on 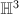 , then
, then  is called a Kleinian group. If
is called a Kleinian group. If  is torsion-free, then
is torsion-free, then 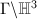 is a hyperbolic manifold.
is a hyperbolic manifold.
 acts isometrically and transitively on
acts isometrically and transitively on 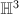 and
and  . So Kleinian groups can be also defined as discrete subgroups of
. So Kleinian groups can be also defined as discrete subgroups of  .
.
We can define similar notions of Kleinian groups like Dirichlet fundamental domains (bounded by geodesic hypersurfaces) and geometrically finiteness. However, unlike the case of Fuchsian groups, a Kleinian group  is finitely generated implies neither its Dirichlet fundamental domains are bounded by finitely many geodesic sides nor
is finitely generated implies neither its Dirichlet fundamental domains are bounded by finitely many geodesic sides nor  is geometrically finite. So Proposition 11 is special for Fuchsian groups.
is geometrically finite. So Proposition 11 is special for Fuchsian groups.
The first geometric method due to Poincaré is the reverse procedure of obtaining a fundamental domain for a group  (see [2] for details).
(see [2] for details).
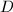 in
in 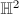 and a pairing of geodesic sides of
and a pairing of geodesic sides of 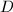 by elements of
by elements of 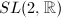 , then under a suitable conditions, these side-pairing elements generate a Fuchsian group such that
, then under a suitable conditions, these side-pairing elements generate a Fuchsian group such that 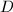 is a fundamental domain.
is a fundamental domain.
The second algebraic method depends on the notion of arithmetic subgroups.
 of
of 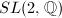 is called an arithmetic subgroup if
is called an arithmetic subgroup if  is commensurable with
is commensurable with 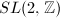 . For an arithmetic subgroup
. For an arithmetic subgroup  , we get a finite common cover
, we get a finite common cover 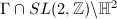 for
for 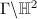 and
and 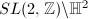 . The examples of arithmetic subgroups of
. The examples of arithmetic subgroups of 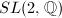 include congruence subgroup of
include congruence subgroup of 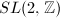 and finite index subgroup of
and finite index subgroup of 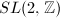 .
.
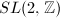 a congruence subgroup?
a congruence subgroup?
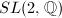 that are not congruence subgroups. However, the answer to the same question for
that are not congruence subgroups. However, the answer to the same question for 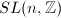 (
(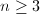 ) is YES due to Bass-Milnor-Serre.
) is YES due to Bass-Milnor-Serre.
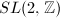 is not uniform. Fuchsian groups commensurable with
is not uniform. Fuchsian groups commensurable with 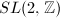 i.e., arithmetic subgroups, are not uniform as they share a common cover with
i.e., arithmetic subgroups, are not uniform as they share a common cover with 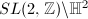 . Is there any algebraic method to construct uniform Fuchsian groups?
. Is there any algebraic method to construct uniform Fuchsian groups?
So far, we have restricted to subgroups of 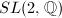 . In order to construct unifomr Fuchsian groups algebraically, we need to find discrete subgroups that are not commensurable to
. In order to construct unifomr Fuchsian groups algebraically, we need to find discrete subgroups that are not commensurable to 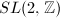 . Let
. Let  be two lattices, then
be two lattices, then  are commensurable if and only if they define the same
are commensurable if and only if they define the same 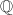 -structure on
-structure on  , i.e.,
, i.e.,  . So to construct uniform lattices of
. So to construct uniform lattices of 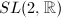 , we need a different
, we need a different 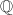 -structure on
-structure on 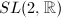 , namely quaternion division algebras over
, namely quaternion division algebras over 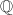 . Those Riemann surfaces constructed in this way are called Shimura curves. André Weil proved that these together with the arithmetic subgroups of
. Those Riemann surfaces constructed in this way are called Shimura curves. André Weil proved that these together with the arithmetic subgroups of 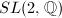 exhaust all the arithmetic subgroups of
exhaust all the arithmetic subgroups of 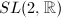 .
.
To define the general notion of arithmetic subgroups of 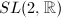 (or a real Lie group), we need to introduce the notion of algebraic groups.
(or a real Lie group), we need to introduce the notion of algebraic groups.
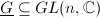 is called an algebraic group if
is called an algebraic group if 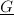 is subvariety, i.e., it is a closed subset defined by a set of polynomial equations.
is subvariety, i.e., it is a closed subset defined by a set of polynomial equations. 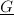 is called to be defined over
is called to be defined over  if the coefficients of the defining polynomials are in
if the coefficients of the defining polynomials are in  .
.
Assume 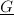 is a linear algebraic group defined over
is a linear algebraic group defined over  . Weil showed that
. Weil showed that  is a Lie group with finitely many connected components.
is a Lie group with finitely many connected components.
 is a semisimple Lie group, then any arithmetic subgroup
is a semisimple Lie group, then any arithmetic subgroup  of
of  is a lattice.
is a lattice.
 an arithmetic subgroup with respect to a suitable
an arithmetic subgroup with respect to a suitable  -structure on
-structure on  ?
?
The answer is NO for 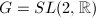 by the Teichmuller theory. In almost all other cases, the answer is YES due to Margulis, which relies on a long line of his work on the rigidity of discrete subgroups. More precisely, we have:
by the Teichmuller theory. In almost all other cases, the answer is YES due to Margulis, which relies on a long line of his work on the rigidity of discrete subgroups. More precisely, we have:
 is a semisimple Lie group without compact factor of rank
is a semisimple Lie group without compact factor of rank 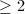 , then any irreducible lattice of
, then any irreducible lattice of  is an arithmetic subgroup.
is an arithmetic subgroup.
References
[1]Discontinuous groups, Annals of Mathematics 44 (1943), no.4, 674--689.
[2]The Geometry of Discrete Groups (Graduate Texts in Mathematics) (v. 91), Springer, 1983.
 ).
).
 .
.
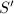 be two generating sets of
be two generating sets of 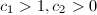 such that for any
such that for any 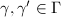 ,
, 
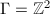 ,
, 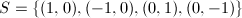 . Then
. Then 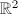 and is not simply connected.
and is not simply connected.
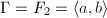 ,
, 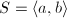 . Then
. Then 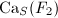 is a infinite tree, hence simply connected.
is a infinite tree, hence simply connected.
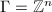 ,
, 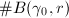 grows polynomially, but for
grows polynomially, but for 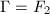 , it grows exponentially.
, it grows exponentially.
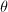 is a homeomorphism if and only if
is a homeomorphism if and only if 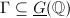 is called an arithmetic subgroup if
is called an arithmetic subgroup if 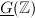 .
.
 .
.