We start by recalling the main theorem of this seminar (Weil II for curves) and illustrating some of its arithmetic consequences. Then we introduce the theory of Lefschetz pencils and deduce the last part (Riemann hypothesis) of the Weil conjectures. Finally, we prove the geometric semisimplicity of lisse pure sheaves, and use it to deduce the hard Lefschetz theorem.
This is an expanded note prepared for a STAGE talk, Spring 2014. Our main references are [1], [2] and [3].
 Weil II for curves
Weil II for curves
Recall that we have proved the following target theorem.
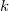 be a finite field and
be a finite field and 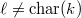 be a prime number. Fix an embedding
be a prime number. Fix an embedding 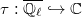 . Let
. Let  be smooth geometrically connected curve. Let
be smooth geometrically connected curve. Let 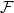 be a lisse
be a lisse  -sheaf on
-sheaf on 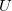 ,
,  -pure of weight
-pure of weight  . Then
. Then
 is
is  -pure of weight
-pure of weight  .
. is
is  -mixed of weight
-mixed of weight  .
. is
is  -pure of weight
-pure of weight  .
.
- Via a series of elementary reductions, reduce to the case
 (at the cost of making the sheaf
(at the cost of making the sheaf 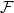 more complicated) and
more complicated) and 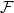 is lisse geometrically irreducible pure of weight 0.
is lisse geometrically irreducible pure of weight 0. - Fix
 , put
, put 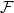 in a 2-variable family
in a 2-variable family  over
over  by Artin-Schreier twists. It suffcies to show that that
by Artin-Schreier twists. It suffcies to show that that  is pure of weight 1 (the purity theorem) for
is pure of weight 1 (the purity theorem) for  and take the limit
and take the limit  (weight dropping).
(weight dropping). - Now fix
 and
and 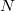 . To show the purity theorem, put
. To show the purity theorem, put  in a 2-variable family
in a 2-variable family  over
over  encoding
encoding  at each fiber.
at each fiber.  is lisse and has geometric monodromy either a finite irreducible subgroup of
is lisse and has geometric monodromy either a finite irreducible subgroup of  or a finite index subgroup containing
or a finite index subgroup containing  (the monodromy theorem). The monodromy theorem reduces to the computation of the 4th moment of
(the monodromy theorem). The monodromy theorem reduces to the computation of the 4th moment of  , which in turn results from the computation
, which in turn results from the computation  .
. - Choosing a space filling curve
 in
in  , the big monodromy forces
, the big monodromy forces  to be pure of weight 2 (Frobenius acts on the geometric coinvariants via roots of unity) and so the
to be pure of weight 2 (Frobenius acts on the geometric coinvariants via roots of unity) and so the  -series
-series  is analytic in
is analytic in  . Now Rankin's trick implies that
. Now Rankin's trick implies that  dominates each term
dominates each term  , hence the latter is also holomorphic in
, hence the latter is also holomorphic in  . The tensor power trick then shows that
. The tensor power trick then shows that  is pure of weight 1, i.e., the purity theorem is true.
is pure of weight 1, i.e., the purity theorem is true.
 : By Leray or Gysin, we have
: By Leray or Gysin, we have  , which consists of the
, which consists of the  -invariants, is
-invariants, is  -pure of weight
-pure of weight  . (Note: cohomology groups are always understood as taking the cohomology of the base change
. (Note: cohomology groups are always understood as taking the cohomology of the base change  ).
). : By Leray or Gysin, we have
: By Leray or Gysin, we have  . Since
. Since  is
is  -mixed of weight
-mixed of weight  , and by Poincare duality,
, and by Poincare duality,  is
is  -mixed of weight
-mixed of weight  , it follows
, it follows  is
is  -pure of weight
-pure of weight  .
. : by birational invariance of top
: by birational invariance of top  (or long exact sequence associated to
(or long exact sequence associated to  ), we have
), we have  , which is
, which is  -pure of weight
-pure of weight  .
¡õ
.
¡õ
 by any morphism
by any morphism  between any separated
between any separated ![$\mathbb{Z}[1/\ell]$](./latex/latex2png-WeilII_73189216_-5.gif) -schemes of finite type and
-schemes of finite type and 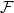 by any
by any  -mixed constructible
-mixed constructible  -sheaf of weight
-sheaf of weight  . Then the constructible
. Then the constructible  -sheaf
-sheaf  on
on  is
is  -mixed of weight
-mixed of weight  for any
for any 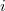 . The weaker Theorem 1 is nevertheless strong enough to deduce the last part (the Riemann hypothesis) of the Weil conjectures.
. The weaker Theorem 1 is nevertheless strong enough to deduce the last part (the Riemann hypothesis) of the Weil conjectures.
Several remarkable arithmetic consequences follows.
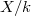 be a smooth projective geometrically connected variety. Then for any
be a smooth projective geometrically connected variety. Then for any 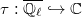 and any
and any 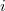 ,
, 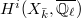 is
is  -pure of weight
-pure of weight 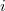 .
.
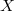 over a finite field
over a finite field 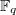 is controlled by the topology of the corresponding complex manifold
is controlled by the topology of the corresponding complex manifold  . If we factorize the zeta function of
. If we factorize the zeta function of 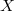 as
as 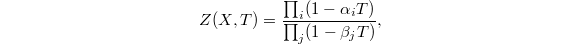 here
here 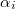 (resp.
(resp. 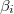 ) are the
) are the 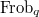 eigenvalues on the odd (resp. even) degree cohomology groups
eigenvalues on the odd (resp. even) degree cohomology groups 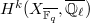 , then by the Lefschetz trace formula,
, then by the Lefschetz trace formula, 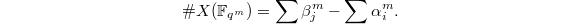 The Riemann hypothesis provides the key to understand these
The Riemann hypothesis provides the key to understand these 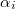 and
and 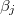 : it allows us to obtain very good estimates of
: it allows us to obtain very good estimates of 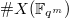 as long as we know enough about the cohomology of
as long as we know enough about the cohomology of 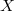 . For example, when
. For example, when 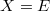 is an elliptic curve over
is an elliptic curve over 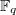 , we obtain
, we obtain 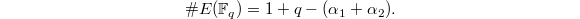 By Corollary 1, we know that
By Corollary 1, we know that 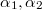 , as
, as 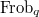 eigenvalues on
eigenvalues on 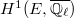 , has pure weight 1. In this way we recover the classical Hasse-Weil bound,
, has pure weight 1. In this way we recover the classical Hasse-Weil bound, 
 -function is defined to be the coefficients of the
-function is defined to be the coefficients of the 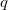 -expansion of the weight 12 cusp eigenform
-expansion of the weight 12 cusp eigenform 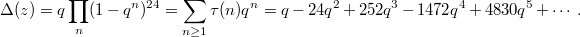 Ramanujan famously observed (!) without proof that
Ramanujan famously observed (!) without proof that 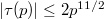 . This turns out to be a general phenomenon for coefficients of a cusp eigenform
. This turns out to be a general phenomenon for coefficients of a cusp eigenform 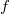 of weight
of weight 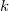 and level
and level 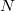 , as a consequence of Weil II together with the algebro-geometric incarnation of cusp eigenforms. Let
, as a consequence of Weil II together with the algebro-geometric incarnation of cusp eigenforms. Let  be the modular curves over
be the modular curves over ![$\mathbb{Z}[1/N]$](./latex/latex2png-WeilII_136422478_-5.gif) with the universal family of elliptic curves
with the universal family of elliptic curves 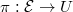 . By the Eichler-Shimura relation, the Hecke eigenvalue
. By the Eichler-Shimura relation, the Hecke eigenvalue 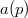 (
(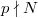 ) of
) of 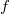 matches up with the trace of
matches up with the trace of 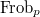 on the (2-dimensional)
on the (2-dimensional) 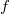 -isotypic component of
-isotypic component of 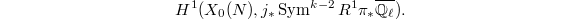 Since
Since 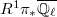 is lisse on
is lisse on 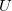 of pure of weight 1, by Corollary 1, the above
of pure of weight 1, by Corollary 1, the above 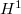 is pure of weight
is pure of weight 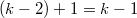 . Therefore both
. Therefore both 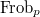 eigenvalues have absolute values
eigenvalues have absolute values 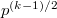 and so
and so 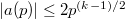 .
.
Notice in this example, it is convenient to work with non-constant coefficient systems. Here is another typical example.
 . The classical Kloosterman sum is defined to be
. The classical Kloosterman sum is defined to be 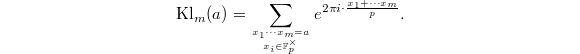 This can be interpreted geometrically as follows. Let
This can be interpreted geometrically as follows. Let  be the Artin-Schrier sheaf on
be the Artin-Schrier sheaf on  associated to the additive character
associated to the additive character 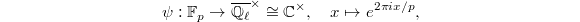 Let
Let 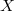 be the smooth affine variety of dimension
be the smooth affine variety of dimension 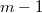 defined by the equation
defined by the equation 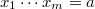 and define
and define 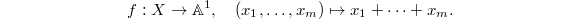 Then
Then 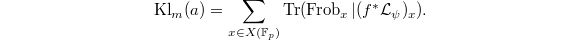 Deligne computed that
Deligne computed that 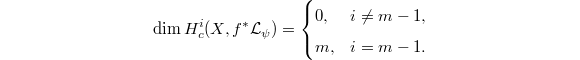 Hence by the strong version of Weil II, we obtain the estimate
Hence by the strong version of Weil II, we obtain the estimate 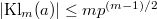 , which is certainly not easy to obtain using elementary methods.
, which is certainly not easy to obtain using elementary methods.
 Lefschetz pencils and Riemann Hypothesis
Lefschetz pencils and Riemann Hypothesis
When 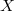 is a curve, the Riemann hypothesis follows from Corollary 1, since
is a curve, the Riemann hypothesis follows from Corollary 1, since  is
is  -pure of weight 0 for any
-pure of weight 0 for any  . For the general case, we induct on
. For the general case, we induct on  via the theory of Lefschetz pencils.
via the theory of Lefschetz pencils.
 be a smooth projective variety of dimension
be a smooth projective variety of dimension  . A Lefschetz pencil of hyperplanes on
. A Lefschetz pencil of hyperplanes on 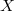 , is a family of hyperplanes
, is a family of hyperplanes  , where
, where ![$H_{[a:b]}=\{a\cdot f+b\cdot g=0\}$](./latex/latex2png-WeilII_130781375_-6.gif) , such that
, such that
- The hyperplane section
 is smooth for all
is smooth for all  in an open dense subset
in an open dense subset  .
. - For
 ,
,  has only one singular point and the singularity is an ordinary double point, i.e., its complete local ring of is the form
has only one singular point and the singularity is an ordinary double point, i.e., its complete local ring of is the form ![$k[ [T_1,\ldots, T_{n+1}] ]/(q(T_1,\ldots, T_{n+1}))$](./latex/latex2png-WeilII_64381355_-5.gif) , where
, where 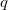 is a non-degenerate quadratic form.
is a non-degenerate quadratic form. - The axis of the pencil
 (of codimension 2 in
(of codimension 2 in  ) intersects with
) intersects with 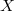 transversely (so
transversely (so  has dimension
has dimension  ).
).
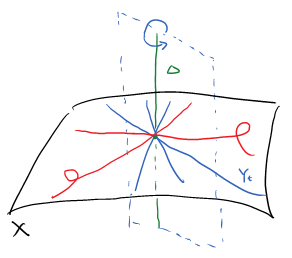
Using incidence correspondences and the Bertini theorem, one can show the existence of Lefschetz pencils.
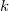 on
on 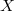 , after possibly a finite extension of the base field and possibly replacing the projective embedding from
, after possibly a finite extension of the base field and possibly replacing the projective embedding from 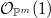 by
by  for some
for some 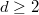 .
.
Let  be the blow up of
be the blow up of 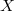 along
along  , then we obtain a projective morphism
, then we obtain a projective morphism  with smooth fibers over
with smooth fibers over  , where
, where 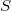 is a finite set of points. After possibly a finite base extension, we may assume
is a finite set of points. After possibly a finite base extension, we may assume 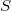 consists of
consists of 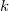 -rational points. The Leray spectral sequence for the blow up
-rational points. The Leray spectral sequence for the blow up  implies that
implies that  So it suffices to prove the purity statement for
So it suffices to prove the purity statement for  .
.
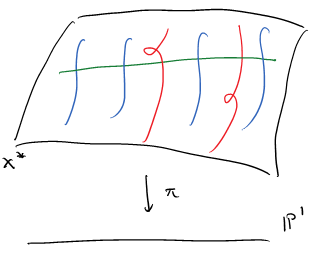
Due to the simple nature of singularities, it is possible to describe both the local and global monodromy actions on the cohomology. In the complex setting, this is classically known as the Picard-Lefschetz theory. In the  -adic setting, this is done in SGA 7 and is briefly summarized as follows.
-adic setting, this is done in SGA 7 and is briefly summarized as follows.
 be the local monodromy group at
be the local monodromy group at  (i.e., the tame quotient of the etale fundamental group of
(i.e., the tame quotient of the etale fundamental group of  ). Let
). Let  be the geometric generic fiber and
be the geometric generic fiber and  be the geometric fiber at
be the geometric fiber at  . Then
. Then
- For
 ,
,  and
and  acts on
acts on  trivially. Namely, away from the middle degree, the singularity at
trivially. Namely, away from the middle degree, the singularity at  is not seen.
is not seen. - The action of
 on
on  is described by the Picard-Lefschetz formula in terms of the intersection pairing with the vanishing cycle at
is described by the Picard-Lefschetz formula in terms of the intersection pairing with the vanishing cycle at  . When
. When  is odd,
is odd,  ; when
; when  is even, either
is even, either  , or we have an exact sequence
, or we have an exact sequence 
 (the invariants under the global geometric monodromy).
(the invariants under the global geometric monodromy).
Now we can finish the induction step. For simplicity let us assume  is odd (the even case is similar). Let
is odd (the even case is similar). Let  and
and  . Then by the property of the Lefschetz pencil (Theorem 3 a), b)), we have
. Then by the property of the Lefschetz pencil (Theorem 3 a), b)), we have  . The Leray spectral sequence implies that
. The Leray spectral sequence implies that  By induction and proper base change,
By induction and proper base change,  is lisse on
is lisse on  , pure of weight
, pure of weight  . So Corollary 1 implies that each term
. So Corollary 1 implies that each term  is pure of weight
is pure of weight  . Hence
. Hence  is pure of weight
is pure of weight  as well. This completes the proof of Theorem 2.
as well. This completes the proof of Theorem 2.
 The hard Lefschetz theorem
The hard Lefschetz theorem
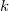 be a finite field and
be a finite field and 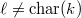 be a prime number. Let
be a prime number. Let 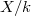 be a smooth geometrically connected variety. Let
be a smooth geometrically connected variety. Let 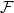 be a lisse
be a lisse  -pure
-pure  -sheaf on
-sheaf on 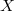 . Then the representation
. Then the representation 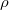 of
of 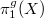 associated to
associated to 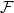 is semisimple.
is semisimple.
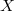 by a space filling curve without changing the geometric monodromy group, the smallest algebraic group containing the image of
by a space filling curve without changing the geometric monodromy group, the smallest algebraic group containing the image of  . So it suffices to treat the curve case. We are going to induct on the length of
. So it suffices to treat the curve case. We are going to induct on the length of 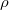 as a
as a 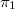 -representation. When
-representation. When 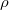 is irreducible as a
is irreducible as a 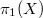 -representation, as in Kestutis's talk,
-representation, as in Kestutis's talk, 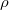 is semisimple as a
is semisimple as a 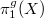 -representation (since
-representation (since 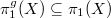 is normal). Now suppose
is normal). Now suppose 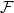 is an extension of lisse
is an extension of lisse  -pure sheaves on
-pure sheaves on 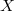 ,
, 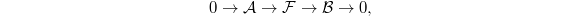 we would like to show that there is a section (as
we would like to show that there is a section (as 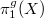 -representations). In other words, we would like to show that the element
-representations). In other words, we would like to show that the element  corresponding to the identity morphism
corresponding to the identity morphism 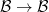 lies in the image of the first map in the following sequence,
lies in the image of the first map in the following sequence,  The crucial thing is the mismatch of weights in the second map: by Theorem 1, the source has weight 0 but the target has weight 1. Since
The crucial thing is the mismatch of weights in the second map: by Theorem 1, the source has weight 0 but the target has weight 1. Since 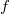 is fixed by
is fixed by 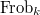 , it must die in
, it must die in 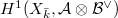 and hence comes from some element of
and hence comes from some element of 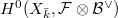 .
¡õ
.
¡õ
Next we will see how the geometric semisimplicity grew out of the arithmetic consideration of weights can help us to understand the fundamental geometric structure of smooth projective varieties.
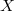 be a projective smooth connected variety over an algebraically closed field (of any characteristic). Let
be a projective smooth connected variety over an algebraically closed field (of any characteristic). Let 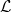 be an ample line bundle on
be an ample line bundle on 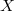 and
and 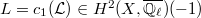 . Then for any
. Then for any 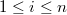 , the
, the 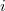 -th iterated cup product
-th iterated cup product 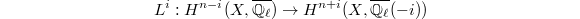 is an isomorphism.
is an isomorphism.
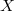 and
and 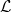 are defined over a finitely generated subfield
are defined over a finitely generated subfield 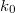 of
of 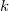 , using the defining equations, we obtain a morphism of scheme
, using the defining equations, we obtain a morphism of scheme 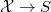 and an ample line bundle on
and an ample line bundle on  with the generic fiber
with the generic fiber 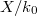 and
and 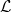 , where
, where 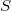 is scheme of a finite type over
is scheme of a finite type over 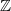 . After possibly shrinking
. After possibly shrinking 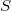 , we may assume
, we may assume 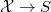 has projective smooth connected fibers. To show
has projective smooth connected fibers. To show 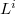 is an isomorphism on over generic point, it suffices to check it is an isomorphism on each closed point. This puts us in the situation where
is an isomorphism on over generic point, it suffices to check it is an isomorphism on each closed point. This puts us in the situation where 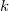 is the algebraic closure of a finite field (even if we work with
is the algebraic closure of a finite field (even if we work with 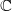 at the beginning).
at the beginning).
The case  is trivial. We are going to induct on the dimension of
is trivial. We are going to induct on the dimension of 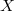 . Take a Lefschetz pencil
. Take a Lefschetz pencil  on
on 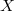 . Let
. Let  be a smooth hyperplane section. By the Lefschetz hyperplane theorem,
be a smooth hyperplane section. By the Lefschetz hyperplane theorem,  is an isomorphism when
is an isomorphism when  and is an injection when
and is an injection when  (I am going to omit all the Tate twists due to my laziness). Taking Poincare dual,
(I am going to omit all the Tate twists due to my laziness). Taking Poincare dual,  is an isomorphism when
is an isomorphism when  and is surjective when
and is surjective when  . Now by the projection formula,
. Now by the projection formula, 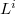 can be decomposed as
can be decomposed as ![$$\xymatrix{H^{n-i}(X) \ar[r]^{L^{i-1}} \ar[d]^{f^*}& H^{n+i-2}(X) \ar[d]^{f^*} \ar[r]^{L} & H^{n+i}(X) \\ H^{n-i}(Y) \ar[r]^{L^{i-1}} & H^{n+i-2}(Y) \ar[ru]^-{f_*}& }.$$](./latex/latex2png-WeilII_205381592_.gif) When
When  ,
,  and
and  are isomorphisms. By induction hypothesis,
are isomorphisms. By induction hypothesis,  is an isomorphism and it follows that
is an isomorphism and it follows that 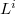 is also an isomorphism. It remains to treat the key case
is also an isomorphism. It remains to treat the key case  . In this case,
. In this case,  is an injection and
is an injection and  is a surjection. By Poincare duality,
is a surjection. By Poincare duality,  is an isomorphism is equivalent to that the pairing
is an isomorphism is equivalent to that the pairing  is non-degenerate. Using the injection
is non-degenerate. Using the injection  , it is equivalent to that the pairing
, it is equivalent to that the pairing  is non-degenerate on the image of
is non-degenerate on the image of  . By the property of the Lefschetz pencil (Theorem 3 c)), we have
. By the property of the Lefschetz pencil (Theorem 3 c)), we have  Now we use Theorem 5: the
Now we use Theorem 5: the  -action on
-action on  is semisimple (this is the only place we use Weil II). So we obtain a
is semisimple (this is the only place we use Weil II). So we obtain a  -equivariant decomposition
-equivariant decomposition  for some
for some  without trivial
without trivial  -constituents. Hence the non-degenerate cup product pairing on
-constituents. Hence the non-degenerate cup product pairing on  decomposes accordingly and in particular restricts to a non-degenerate pairing on
decomposes accordingly and in particular restricts to a non-degenerate pairing on  , as desired.
¡õ
, as desired.
¡õ
We mention one immediate geometric consequence of the hard Lefschetz theorem to end this talk.
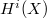 , which is alternating when
, which is alternating when 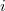 is odd.
¡õ
is odd.
¡õ
References
[1]L-functions and monodromy: four lectures on Weil II, 2000, http://web.math.princeton.edu/~nmk/arizona34.pdf.
[2]Lectures on Etale Cohomology (v2.10), Available at www.jmilne.org/math/.
[3]La conjecture de Weil. II, Inst. Hautes &EACUTE;tudes Sci. Publ. Math. (1980), no.52, 137--252.
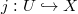 be a smooth compactification over
be a smooth compactification over 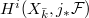 is
is 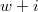 for
for 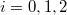 .
.
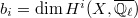 is even for odd
is even for odd