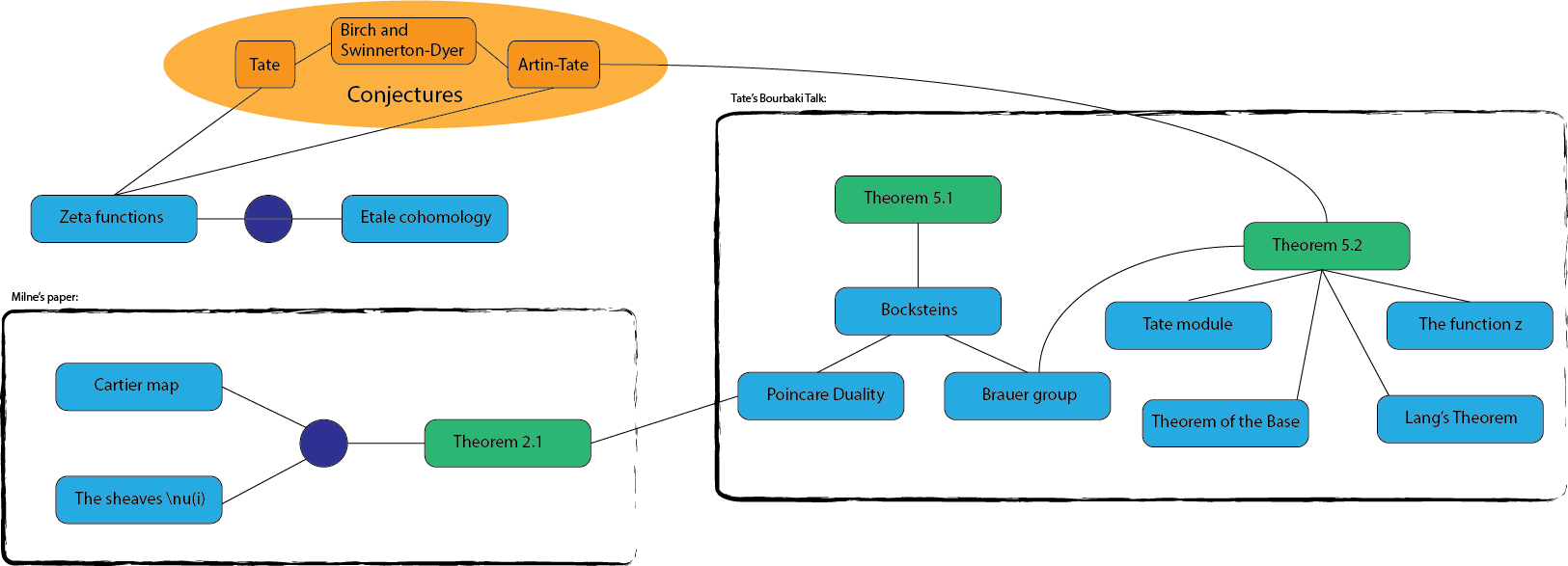
This is a concept map for the Tate conjecture seminar, organized by Yiwei She, Daniel Litt, David Hansen and Johan de Jong, which will be on the Tate conjecture for surfaces over finite fields and mainly on a paper by Milne on this topic. The talks will be given by the organizers and some of the participants. As the lectures progress, this page will be populated with many of the important concepts and relationships between them.
This page is maintained by Daniel Halpern-Leistner, with concept bubbles submitted each week by the speakers (or anyone else). To submit bubbles, please follow this template. You can just include in the body of an email.

Zeta Functions
Zeta functions can be defined for varieties over finite fields and with a bit more work for varieties over number fields. For a smooth projective variety $X$ over a finite field $k$ with $q$ elements the definition is the following Euler product $$ \zeta_X(s) = \prod_{x \in X\text{ closed}} (1 - \# \kappa(x) q^{-s})^{-1} $$ For the projective line we obtain for example $(1 - q^{-s})^{-1} (1 - q^{1 - s})^{-1}$.
Etale Cohomology
Etale cohomology can be used to construct a Weil cohomology theory for smooth projective varrieties over any field $k$. This is done by picking a prime number $\ell$ different from the characteristic of $k$ and setting $$ H^i(X) = H^i_{et}(X_{\overline{k}}, \mathbf{Q}_\ell) = \left(\lim H^i_{et}(X_{\overline{k}}, Z/\ell^n Z) \right) \otimes_{\mathbf{Z}_\ell} \mathbf{Q}_\ell $$ An important feature of these cohomology groups is that the absolute Galois group of $k$ acts on them.
Connection Zeta functions and Etale Cohomology
Let $k$ be a finite field with $q$ elements and let $X$ be a smooth projective variety over $k$. For any Weil cohomology theory $H^*$ there is a connection between the Zeta function of $X$ and cohomology. Namely, we have $$ \zeta_X(s) = \prod_i \det(1 - \pi_X^* q^{-s}|_{H^i(X)})^{(-1)^{i + 1}} $$
Tate Conjecture
The Tate conjecture predicts that a cohomology class in $l$-adic etale cohomology which is fixed under the action of the Galois group should be algebraic if the ground field is finitely generated over the prime field. If the ground field is finite, then the Tate conjecture in its strongest form says that the rank of the Chow group of codimension $i$ cycles modulo numerical equivalence is equal to the order of pole of $\zeta_X(s)$ at $s = i$.
Good reference: Tate's paper ``Conjectures on algebraic cycles in $l$-adic cohomology'', available in this volume.
Birch and Swinnerton-Dyer conjecture
The Birch and Swinnerton-Dyer conjecture says first that the rank of the group $A(K)$ of rational points of an abelian variety $A$ over a global field $K$ can be determined by the number of points on the good reductions of $A$ at the finite places. More precisely, the order of pole of the L-function of $A$ at $s = 1$ should be the rank. Moreover, it predicts a the leading coefficient of the expansion of the L-function at $s = 1$ roughly in terms of torsion in $A(K)$, the height pairing on $A(K)$, an integral of a top form, and the Shafarevich group of $A/K$.
Artin-Tate Conjecture
The Artin-Tate conjecture is a geometric analogue of the Birch and Swinnerton-Dyer conjecture for surfaces $X$ over a finite field $k$. It was invented by translating the prediction of BSD when $X$ is an elliptic surface (or more generally fibres over a curve) into invariants not depending on the chosen fibration. Roughly the Artin-Tate conjecture predicts, assuming the strong form of the Tate conjecture, that the leading coefficient of $\zeta_X(s)$ at $s = 1$ looks like $$ \frac{ \# Br(X) | \det(D_iD_j) | }{ q^{\alpha(X)} \# NS(X)_{tors} } $$ Here $Br(X)$ is the Brauer group of $X$ which is conjectured to be finite in order to make sense of the conjecture. The term $\det(D_iD_j)$ is essentially the discriminant of the intersection pairing on the Neron-Severi group $NS(X)$ and $\alpha(X) = \chi(X, O_X) - 1 + \dim(Pic^0(X))$.
Brauer Group
The "cohomological Brauer group" is defined as $\text{Br}(X):=H^2(X, \mathbb{G}_m)_{\text{tors}}.$ For quasi-projective schemes this agrees with the usual definition: Azumaya algebras modulo Morita equivalence.
Theorem 5.1 of Tate
Let $X$ be a smooth projective surface over a finite field $k$. There is a skew-symmetric pairing $$\text{Br}(X)[\ell^\infty]\times \text{Br}(X)[\ell^\infty]\to \mathbb{Q}_\ell/\mathbb{Z}_\ell$$ whose kernel is exactly the divisible elements, if $\ell$ is prime to the characteristic of $k$.
The point of this theorem is to show that the order of the Brauer group (away from the characteristic of $k$) is a square or twice a square, by analogy to the Tate-Shafarevic group. Milne's paper will show that the assumption on $\ell$ is unnecessary.
Poincare Duality
The pairing in Theorem $5.1$ comes from an arithmetic analogue of Poincare duality. In the case of a smooth projective surface $X$ over $\bar k$ (the algebraic closure of a finite field), Poincare duality is a perfect pairing $$H^i(X, \mu_n)\times H^{4-i}(X, \mu_n)\to H^4(X, \mu_n^{\otimes 2})\simeq \mathbb{Z}/n\mathbb{Z},$$ induced by the cup product, for $n$ prime to the characteristic of $k$.
We use this and some Galois cohomology to deduce that for $X$ a smooth projective surface over $k$, the cup product induces a perfect pairing $$H^i(X, \mu_n)\times H^{5-i}(X, \mu_n)\to H^5(X, \mu_n^{\otimes 2})\simeq \mathbb{Z}/n\mathbb{Z}.$$ Loosely speaking, $X$ should be viewed as a $5$-manifold rather than a $4$-manifold, because the cohomological dimension of $k$ is one.
Bocksteins
The short exact sequence of etale sheaves $$1\to \mu_m\to \mu_{m^2}\to \mu_m\to 1$$ induces a long exact sequence in cohomology; the boundary homomorphism $\delta$ is called the Bockstein.
The relevance to Theorem 5.1 of Tate is that Arithmetic Poincare duality induces a perfect pairing $$H^2(X, \mu_m)\times H^3(X, \mu_m)\to \mathbb{Z}/m\mathbb{Z}.$$ The Bockstein exhibits $$A_m:={\rm Br}(X)[m]/m{\rm Br}(X)[m^2]$$ as a quotient of $H^2(X, \mu_m)$ and a subspace of $H^3(X, \mu_m)$. The induced pairing makes $A_m$ self-dual; analyzing this pairing and taking the direct limit over all $m$ prime to the characteristic proves the Theorem.
Theorem 5.1 of Tate
States that for $l \neq {\rm char} k$, the finiteness of ${\rm Br}(X)(l)$, the $l$-power torsion, is equivalent to any of the following
Theorem of the Base
This states that $NS(X)$ is finitely generated for a smooth projective variety over any field.
Lang's Theorem
This states that $H^1(G,{\rm Pic}^0(\bar{X})) = 0$ for a smooth projective surface over a finite field $k$, where $G$ is the absolute Galois group of $k$.
The Tate construction
Given an abelian group (or a $G$-module) $M$, the Tate module is defined to be $$T_l(M) := \varprojlim_n M_{l^n} \simeq {\rm Hom}(\bQ_l / \bZ_l,M),$$ where $M_{l^n}$ denotes the $l^n$-torsion. This is a $\mathbb{Z}_l$-module with the property that $$T_l(M) = T_l(M(l)^{div}),$$ where $M(l)^{div}$ denotes the maximal divisible subgroup of the $l$-power torsion of $M$. Note that any torsion $\mathbb{Z}_l$-module is of the form $(\bQ_l / \bZ_l)^{\oplus I} \oplus E$ where the left summand is the maximal divisible subgroup. If $I$ is finite (for instance if $M_l$ is finite), then $T_l(M(l)) = \bZ_l^{\oplus I}$.
We use the notation $$H^2(\bar{X},T_l(\mu)):= \varprojlim_n H^2(\bar{X},\mu_{l^n}).$$ It agrees with $H^2(\bar{X},\bZ_l)$ as a $\bZ_l$-module, but the eigenvalues of Frobenius on the former are multiplied by $q^{-1}$. That's why $P_2(X,q^{-1}T)$ shows up.
The function z
For a map of $\bZ_l$-modules $f : M \to N$ whose kernel and cokernel are finite (what Tate calls a ``quasi-isomorphism''), we define $$z(f) := l^{{\rm length}(\ker (f)) - {\rm length}({\rm coker}(f))}.$$ This function has nice properties (is explicitly computable, behaves nicely under composition, dualization, etc). The most important property is that for a finitely generated $\bZ_l$-module $M$ with Galois action, $M^G \to M_G$ is a quasi-isomorphism if and only if $$\det(1-\sigma T|M) = (1-T)^{{\rm rank}(M^G)} \cdot R(T),$$ where $R(T) \neq 0$. Furthermore in this case $|R(1)|_l = z(M^G \to M_G)$.
In the case of the Artin-Tate conjecture, where $M = H^2(\bar{X},T_l(\mu))$, one can compute $z(f)$ and arise at the $l$-adic absolute value of the value of $P_2(X,q^{-1}T) / (1-T)^{\rho(X)}$ at $T=1$ by realizing $f$ as part of a certain commutative diagram and using the formal properties of $z(\bullet)$.
Theorem 2.1 of Milne
Let $X$ be a smooth projective surface over a finite field $k$. There are nondegenerate pairings $$ H^i(X, \mu_{p^n}) \times H^{5 - i}(X, \mu_{p^n}) \longrightarrow \mathbf{Z}/p^n\mathbf{Z} $$ compatible with varying $n$, compatible with the intersection product on divisors, and compatible with Bocksteins.
The cohomology used is flat cohomology (cohomology in the fppf site) and the cohomology groups in question are finite groups.
Cartier Operator
Let $X$ be a scheme in characteristic $p$. There is a map $C^{-1} : \Omega^i_X \to H^i(\Omega_X^\bullet)$ sending the local section $f \text{d}g_1 \wedge \ldots \wedge \text{d}g_i$ to $f^p g_1^{p - 1} \ldots g_i^{p - 1} \text{d}g_1 \wedge \ldots \wedge \text{d}g_i$. Locally any differential is a sum of differentials of the form $f \text{d} \log(g_1) \wedge \cdots \wedge \text{d} \log(g_i)$ with $g_i \in \mathcal{O}^\ast$, the Cartier map becomes $$C^{-1} : f \text{d} \log(g_1) \wedge \cdots \wedge \text{d} \log(g_i) \mapsto f^p \text{d} \log(g_1) \wedge \cdots \wedge \text{d} \log(g_i)$$ If $X$ is smooth over a perfect field, this map is an isomorphism.
Let $B\Omega^i_X \subset Z\Omega^i_X \subset \Omega^i_X$ be the image and kernel of $\text{d}$. In the paper of Milne the operator $$ C : Z\Omega^i_X \longrightarrow \Omega^i_X $$ which is the composition of $Z\Omega^i_X \to H^i(\Omega^\bullet_X)$ with the inverse of the inverse Cartier operator $C:= (C^{-1})^{-1}$ plays an important role.
The sheaves $\nu(i)$
For $X$ smooth over a perfect field of characteristic $p$ the map $1 - C : Z\Omega^i_X \to \Omega^i_X$ is surjective in the \'etale topology and the kernel $\nu(i)$ is locally in the \'etale topology generated by logarithmic differentials.
In particular $\mathcal{O}^*/\mathcal{O}^{*p} = \nu(1)$.
Proof of 2.1 mod $p$
Show that $H^i(X, \mu_p)$ is equal to $H^{i - 1}(X, \nu(1))$. Then use the pairing $\nu(1) \times \nu(1) \to \nu(2)$, $$\left(\text{d}\log(g_1), \text{d}\log(g_2) \right) \mapsto \text{d}\log(g_1) \wedge \text{d}\log(g_2)$$ to get maps into $H^5(X, \nu(2))$. Use the exact sequence $$ 0 \to \nu(2) \to \Omega^2_X \xrightarrow{1 - C} \Omega^2_X \to 0 $$ to relate this to $H^2(X, \Omega^2_X)$ and Serre duality.